Question

【题目】已知函数.

(I)求，的值；

(II)求；

(III)若，求.

Answer 1

【答案】(I),-11 ; (II)f（8x﹣1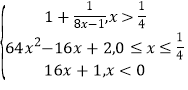）＝;(III)或

【解析】

(I)根据函数的解析式依次求值即可；(II)根据解析式对8x﹣1分三种情况依次求出，最后再用分段函数的形式表示出f（8x﹣1）；(III)根据解析式对4a分三种情况，分别由条件列出方程求出a的值．

(I)由题意得，f（1+）＝f（2+）＝1+

=1+ ，

又f（﹣4）＝﹣8+3＝-5，则f（-5）＝-10+3＝-7，f（-7）＝-14+3＝-11，

所以；

(II)当8x﹣1＞1即x＞时，f（8x﹣1）＝1+，

当﹣1≤8x﹣1≤1即0≤x≤时，f（8x﹣1）＝（8x﹣1）2+1＝64x2﹣16x+2，

当8x﹣1＜﹣1即x＜0时，f（8x﹣1）＝2（8x﹣1）+3＝16x+1，

综上可得，f（8x﹣1）＝ ；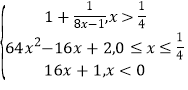

(III)因为，所以分以下三种情况：

当4a＞1时，即a＞时，f（4a）＝＝，解得a＝，成立，

当﹣1≤4a≤1时，即-≤a≤时，f（4a）＝16a2+1＝，解得a＝，成立

当4a＜﹣1时，即a<-时，f（4a）＝8a+3＝，解得a=-，不成立，

综上可得，a的值是或．