练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆，直线过点且与圆相切 .

    （I）求直线的方程；

    （II）如图，圆与轴交于两点，点是圆上异于的任意一点，过点且与轴垂直的直线为，直线交直线于点，直线交直线于点，求证：以为直径的圆与轴交于定点，并求出点的坐标 .

    【答案】（1）.

    （2）证明见解析；定点或.

    【解析】

    （1）由已知中直线过点，我们可以设出直线的点斜式方程，化为一般式方程后，代入点到直线距离公式，根据直线与圆相切，圆心到直线的距离等于半径，可以求出k的值，进而得到直线的方程；

    （2）由已知我们易求出P,Q两个点的坐标，设出M点的坐标，我们可以得到点P与Q的坐标，进而得到以为直径的圆的方程，根据圆的方程即可判断结论.

    (Ⅰ)由题意得，直线的斜率存在.

    设直线的方程为.

    因为直线与圆相切，

    所以.

    所以.

    所以直线方程为.

    (Ⅱ)由题意得，点，点.

    设点，则.

    直线的方程为.

    所以直线与直线的交点为点.

    直线的方程为.

    所以直线与直线的交点为点.

    设点.

    则，.

    因为以为直径的圆与轴交于定点,

    所以

    解得.

    所以定点或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】三棱柱，侧棱与底面垂直，，，，分别是，的中点．

    （）求证：平面．

    （）求证：平面平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设|θ|＜ ，n为正整数，数列{an}的通项公式an=sin tannθ，其前n项和为Sn
    （1）求证：当n为偶函数时，an=0；当n为奇函数时，an=（﹣1） tannθ；
    （2）求证：对任何正整数n，S2n= sin2θ[1+（﹣1）n+1tan2nθ]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表所示:

    商店名称

    A

    B

    C

    D

    E

    销售额(x)/千万元

    3

    5

    6

    7

    9

    利润额(y)/百万元

    2

    3

    3

    4

    5

    (1)画出销售额和利润额的散点图.

    (2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程=x+,其中=,=-.

    (3)若获得利润是4.5百万元时估计销售额是多少(千万元)?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:

    最高

    气温

    [10,

    15)

    [15,

    20)

    [20,

    25)

    [25,

    30)

    [30,

    35)

    [35,

    40)

    天数

    2

    16

    36

    25

    7

    4

    以最高气温位于各区间的频率代替最高气温位于该区间的概率.

    (1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列.

    (2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且满足条件b2+c2﹣a2=bc=1，cosBcosC=﹣ ，则△ABC的周长为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如图显示．

    （1）已知[30，40）、[40，50）、[50，60）三个年龄段的上网购物者人数成等差数列，求a，b的值．
    （2）该电子商务平台将年龄在[30，50）之间的人群定义为高消费人群，其他的年龄段定义为潜在消费人群，为了鼓励潜在消费人群的消费，该平台决定发放代金券，高消费人群每人发放50元的代金券，潜在消费人群每人发放100元的代金券，现采用分层抽样的方式从参与调查的1000位上网购者中抽取10人，并在这10人中随机抽取3人进行回访，求此三人获得代金券总和X的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面ABCD是菱 形，PA＝PB，且侧面PAB⊥平面ABCD，点E是AB的中点.

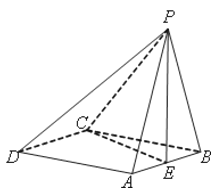
    (1)求证：PE⊥AD；

    (2)若CA＝CB，求证：平面PEC⊥平面PAB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在棱长为的正方体中，，分别是和的中点．

    （）求异面直线与所成角的余弦值．

    （）在棱上是否存在一点，使得二面角的大小为？若存在，求出的长；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案