
 ,求角C;
,求角C;  --------------------------4分
--------------------------4分 ∴B=
∴B= +C,将其代入上式,得sin(
+C,将其代入上式,得sin( +C)=2sinC
+C)=2sinC cosC+cos
cosC+cos sinC=2sinC, -----------------------------5分
sinC=2sinC, -----------------------------5分 sinC=cosC ------------------------- --------6分
sinC=cosC ------------------------- --------6分
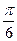 ---------------8分
---------------8分 ------------10分
------------10分 cosC=
cosC= ≥
≥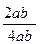 =
= (当且仅当a=b时取等号) ---------------------11分
(当且仅当a=b时取等号) ---------------------11分 ,
, )上递减,∴0<C≤
)上递减,∴0<C≤


科目:高中数学 来源:不详 题型:解答题

 ,
, 的最大值为
的最大值为 .
. 最大时,走了几分钟;
最大时,走了几分钟;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 相距9海里的C处有一艘走私船,正沿南偏东75
相距9海里的C处有一艘走私船,正沿南偏东75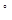 的方向以10海里/小时的速度逃窜.
的方向以10海里/小时的速度逃窜.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 边,向量m=(
边,向量m=( ),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com