
【题目】已知函数![]() ,
, 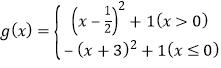 则方程g[f(x)]﹣a=0(a为正实数)的实数根最多有( )个.
则方程g[f(x)]﹣a=0(a为正实数)的实数根最多有( )个.
A.6个
B.4个
C.7个
D.8个
【答案】A
【解析】解:∵函数![]() ,
, 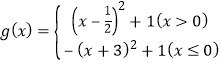 ,
,
令f′(x)=0 可得 x=0,x=2,在(﹣∞,0)上,f′(x)>0,f(x)是增函数;
在(0,2)上,f′(x)<0,f(x)是减函数;在(2,+∞)上,f′(x)>0,f(x)是增函数.
故f(x)的极大值为f(0)=1,极小值为f(2)=﹣3,且函数的值域为R.
由函数g(x)的图象可得,当x=﹣3或x=![]() 时,g(x)=1.
时,g(x)=1.
①当a=1时,若方程g[f(x)]﹣a=0,则:
f(x)=﹣3,此时方程有2个根,或f(x)=![]() , 此时方程有3个根,
, 此时方程有3个根,
故方程g[f(x)]﹣a=0可能共有5个根.
②当0<a<1时,方程g[f(x)]﹣a=0,则:
f(x)∈(﹣4,﹣3),此时方程有1个根,或f(x)∈(﹣3,﹣2),此时方程有3个根
故方程g[f(x)]﹣a=0可能共有4个根.
③当a>1时,方程g[f(x)]﹣a=0,则:f(x)∈(0,![]() ),或f(x)∈(
),或f(x)∈(![]() , +∞),
, +∞),
方程可能有4个、5个或6个根.
故方程g[f(x)]﹣a=0(a为正实数)的实数根最多有6个,
故选 A.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆![]() 的右焦点坐标为
的右焦点坐标为![]() ,求
,求![]() 的值;
的值;
(2)由椭圆![]() 上不同三点构成三角形称为椭圆的内接三角形.若以
上不同三点构成三角形称为椭圆的内接三角形.若以![]() 为直角顶点的椭圆
为直角顶点的椭圆![]() 的内接等腰直角三角形恰有三个,求
的内接等腰直角三角形恰有三个,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
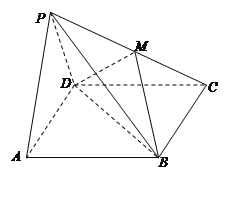
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() ∥面BDM.
∥面BDM.
(1)求直线PC与平面BDM所成角的正弦值;
(2)求平面BDM与平面PAD所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤![]() )的部分图象,其图象与y轴交于点(0,
)的部分图象,其图象与y轴交于点(0,![]() )
)
(Ⅰ)求函数的解析式;
(Ⅱ)若![]() , 求
, 求![]() -
-![]() 的值.
的值.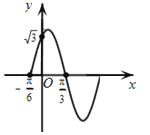
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2ax2﹣2bx﹣a+b(a,b∈R,a>0),g(x)=2ax﹣2b
(1)若![]() 时,求f(sinθ)的最大值;
时,求f(sinθ)的最大值;
(2)设a>0时,若对任意θ∈R,都有|f(sinθ)|≤1恒成立,且g(sinθ)的最大值为2,求f(x)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
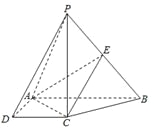
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com