
已知直角三角形的两条直角边长分别为4和6,则这两直角边上的中线所夹的锐角的余弦值是( )
A.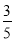 B.
B. 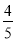 C.
C.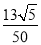 D.
D.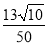
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源:2016届山西省高一下学期期中考试数学试卷(解析版) 题型:填空题
下列命题中:
⑴ 向量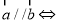 存在唯一的实数
存在唯一的实数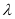 ,使得向量
,使得向量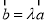 ;
;
⑵ 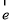 为单位向量,且向量
为单位向量,且向量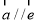 ,则向量
,则向量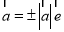 ;
;
⑶ 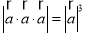 ;
;
⑷ 若向量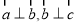 ,则向量
,则向量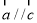 ;
;
⑸ 若向量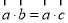 ,则
,则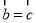 。
。
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2016届山西省高一下学期期中考试数学试卷(解析版) 题型:选择题
为得到函数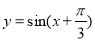 的图像,可将函数
的图像,可将函数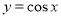 的图像向右平移
的图像向右平移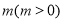 个
个
单位长度,则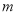 的最小值是( )
的最小值是( )
A.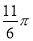 B.
B.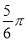 C.
C.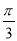 D.
D.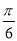
查看答案和解析>>
科目:高中数学 来源:2016届山东省滨州市高一下学期期末考试数学试卷(解析版) 题型:解答题
如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面ACC1A;
(3)求三棱锥C﹣BC1D的体积.
查看答案和解析>>
科目:高中数学 来源:2016届山东省滨州市高一下学期期末考试数学试卷(解析版) 题型:选择题
正方体ABCD﹣A1B1C1D1中AB的中点为M,DD1的中点为N,则异面直线B1M与CN所成的角是( ).
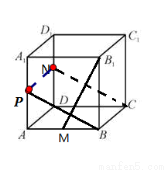
A.0° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一3月质量检测数学试卷(解析版) 题型:选择题
若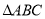 的三个内角满足
的三个内角满足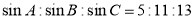 ,则
,则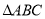 ( )
( )
A.一定是锐角三角形 B.一定是直角三角形
C.一定是钝角三角形 D.可能是锐角三角形,也可能是钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com