
已知函数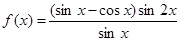 。
。
(1)求 的定义域及最小正周期;
的定义域及最小正周期;
(2)求 的单调递增区间。
的单调递增区间。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
把函数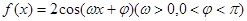 的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移
的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移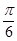 个单位后得到一个最小正周期为
个单位后得到一个最小正周期为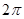 的奇函数
的奇函数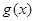 。
。
(1)求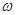 和
和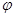 的值
的值
(2)求函数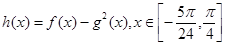 的最大值与最小值。
的最大值与最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在 △ABC内有一内接正方形,它的一条边在斜边BC上,设AB=
△ABC内有一内接正方形,它的一条边在斜边BC上,设AB= ,∠ABC
,∠ABC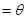

(1)求△ABC的面积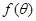 与正方形面积
与正方形面积 ;
;
(2)当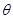 变化时,求
变化时,求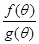 的最小值,并求出对应
的最小值,并求出对应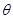 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共9分)
已知函数f(x)=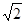 sin(2x+
sin(2x+ ),x∈R.
),x∈R.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[- ,
, ]上的最大值和最小值。
]上的最大值和最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com