
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
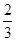 .
.| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
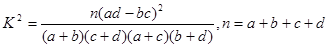
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | 22 | 6 | 28 |
| 女生 | 10 | 10 | 20 |
| 合计 | 32 | 16 | 48 |
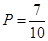 .
.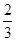 ,可得关注NBA的学生的人数,即可得到列联表;利用公式求得K2,与临界值比较,即可得到结论.
,可得关注NBA的学生的人数,即可得到列联表;利用公式求得K2,与临界值比较,即可得到结论.| | 关注NBA | 不关注NBA | 合计 |
| 男生 | 22 | 6 | 28 |
| 女生 | 10 | 10 | 20 |
| 合计 | 32 | 16 | 48 |
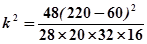
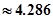 (4分)
(4分)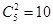 ,共10种,其中甲、乙至少有一人被选中有
,共10种,其中甲、乙至少有一人被选中有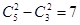 :共7种, 故所求的概率为
:共7种, 故所求的概率为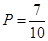 (10分)
(10分)

 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:不详 题型:解答题
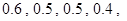 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
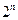 ,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)
,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.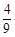 | B.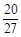 | C.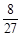 | D.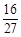 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
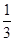 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
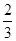 ,乙获胜的概率是
,乙获胜的概率是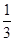 ,则比赛以甲三胜一负而结束的概率为________.
,则比赛以甲三胜一负而结束的概率为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com