练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知直线l经过点P(3，1)，且被两平行直线l1：x＋y＋1＝0和l2：x＋y＋6＝0截得的线段之长为5，求直线l的方程．


    解：(解法1)若直线l的斜率不存在，则直线l的方程为x＝3，此时与l1、l2的交点分别为A′(3，－4)和B′(3，－9)，截得的线段AB的长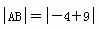＝5，符合题意．

    若直线l的斜率存在，则设直线l的方程为y＝k(x－3)＋1.

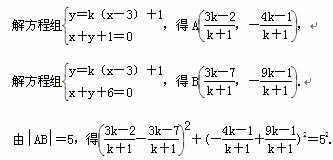    解之，得k＝0，即所求的直线方程为y＝1.

    综上可知，所求l的方程为x＝3或y＝1.

    (解法2)由题意，直线l1、l2之间的距离为d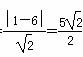＝，且直线l被平行直线l1、l2所截得的线段AB的长为5(如图)．

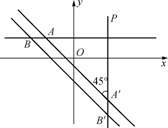
    设直线l与直线l1的夹角为θ，则sinθ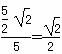＝，故θ＝45°.

    由直线l1：x＋y＋1＝0的倾斜角为135°，知直线l的倾斜角为0°或90°.又直线l过点P(3，1)，故直线l的方程为x＝3或y＝1.

    (解法3)设直线l与l1、l2分别相交于A(x1，y1)、B(x2，y2)，则x1＋y1＋1＝0，x2＋y2＋6＝0.

    两式相减，得(x1－x2)＋(y1－y2)＝5.　①

    又(x1－x2)2＋(y1－y2)2＝25，　②

    联立①②，可得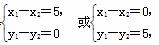

    由上可知，直线l的倾斜角分别为0°或90°.

    故所求直线方程为x＝3或y＝1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知，函数.

    （1）若为偶函数，求的值；

    （2）若，求函数的单调递增区间；

    （3）求函数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     是(　　)

    A．第一象限角  B．第二象限角   C．第三象限角  ．第四象限角

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A，B，C所对的边分别是a，b，c，若sin2B＋sin2C＝sin2A＋sin Bsin C，且＝4，求△ABC的面积S.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若直线l经过直线2x－y＋3＝0和3x－y＋2＝0的交点，且垂直于直线y＝2x－1，则直线l的方程为______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线y＝2x是△ABC中∠C的平分线所在的直线，且A、B的坐标分别为A(－4，2)、B(3，1)，求顶点C的坐标并判断△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     点(1，cosθ)(其中0≤θ≤π)到直线xsinθ＋ycosθ－1＝0的距离是，那么θ等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线y＝kx＋3与圆(x－2)2＋(y－3)2＝4相交于M，N两点，若MN≥2，则k的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列满足：（m为正整数），若，则m所有可能的取值为________。

    查看答案和解析>>

    同步练习册答案