
选修4—4:坐标系与参数方程
自极点O任意作一条射线与直线 相交于点M,在射线OM上取点P,使得
相交于点M,在射线OM上取点P,使得 ,求动点P的极坐标方程,并把它化为直角坐标方程.
,求动点P的极坐标方程,并把它化为直角坐标方程.
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源:2016届广西南宁市高三第二次模拟考试数学(理)试卷(解析版) 题型:解答题
如图,正方体 中,点
中,点 是
是 的中点.
的中点.

(1)求 和平面
和平面 所成角的余弦值;
所成角的余弦值;
(2)在 上找一点
上找一点 ,使得
,使得 平面
平面 .
.
查看答案和解析>>
科目:高中数学 来源:2016届江西萍乡市高三下学期第二次模拟数学(文)试卷(解析版) 题型:选择题
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长是( )

A. B.
B. C.6 D.
C.6 D.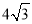
查看答案和解析>>
科目:高中数学 来源:2017届江苏苏州市高三暑假自主学习测试数学试卷(解析版) 题型:解答题
如图,某城市小区有一个矩形休闲广场, 米,广场的一角是半径为
米,广场的一角是半径为 米的扇形
米的扇形 绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅
绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅 (宽度不计),点
(宽度不计),点 在线段
在线段 上,并且与曲线
上,并且与曲线 相切;另一排为单人弧形椅沿曲线
相切;另一排为单人弧形椅沿曲线 (宽度不计)摆放.已知双人靠背直排椅的造价每米为
(宽度不计)摆放.已知双人靠背直排椅的造价每米为 元,单人弧形椅的造价每米为
元,单人弧形椅的造价每米为 元,记锐角
元,记锐角 ,总造价为
,总造价为 元.
元.

(1)试将 表示为
表示为 的函数
的函数 ,并写出
,并写出 的取值范围;
的取值范围;
(2)如何选取点 的位置,能使总造价
的位置,能使总造价 最小.
最小.
查看答案和解析>>
科目:高中数学 来源:2016届湖北华中师大一附中高三五月适应性考试数学文试卷(解析版) 题型:解答题
如图,四棱锥 ,底面
,底面 为直角梯形,
为直角梯形,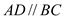 ,
, 底面
底面 ,
,
 为
为 的中点,
的中点, 为棱
为棱 的中点.
的中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)已知 ,求点
,求点 到平面
到平面 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北唐山一中高二下学期期末数学文试卷(解析版) 题型:解答题
已知直线
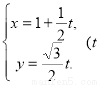 为参数),曲线
为参数),曲线
 (
( 为参数).
为参数).
(1)设 与
与 相交于
相交于 两点,求
两点,求 ;
;
(2)若把曲线 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线
倍,得到曲线 ,设点
,设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com