练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱柱中，平面，，，，，分别为、的中点．

    （1）求证：平面平面；

    （2）求证：平面，并求到平面的距离．

    【答案】（1）证明见解析；（2）证明见解析，．

    【解析】

    试题分析：（1）由勾股定理，得出，再根据平面，利用线面垂直的判定定理，证得平面，即可证明平面平面；（2）取中点，∵为中点，∴，又为中点，四边形为平行四边形，∴，即可得出平面平面，进而得出平面，进而即可求解到平面的距离．

    试题解析：证明：（1）∵，∴，

    又平面，∴，又，∴平面，

    ∵平面，∴平面平面．

    （2）取中点，∵为中点，∴，

    又为中点，四边形为平行四边形，∴，又，

    ∴平面平面．

    ∵平面，∴平面．

    ∴到平面的距离即为到平面的距离．

    过作于，∵平面平面，∴平面，

    ∴．

    ∴点到平面的距离为．（或由等体积法可求）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若A={0,2,4,6},B={0,3,6,9},则A∩B=（ ）
    A.{0}
    B.{6}
    C.{0,6}
    D.{0,3,6}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求的极值；

    （2）若对恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数其图像与轴交于两点，且.

    （1）求的取值范围；

    （2）证明：；（为的导函数；）

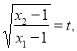    （3）设点C在函数图像上，且△ABC为等腰直角三角形，记求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项均为正数的数列的前项和为，满足：（其中为常数）．

    （1）若，，数列是等差数列，求的值；

    （2）若数列是等比数列，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （I）曲线在x=1处的切线与直线垂直，求实数a的值；

    （II）当时，求证： 在（1，+∞）上单调递增；

    （III）当x≥1时， 恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两工人在同样的条件下生产，日产量相等，每天出废品的情况如下表所列：

    工人

    甲

    乙

    废品数

    0

    1

    2

    3

    0

    1

    2

    3

    概率

    0.4

    0.3

    0.2

    0.1

    0.3

    0.5

    0.2

    0

    则有结论（　　）

    A．甲的产品质量比乙的产品质量好一些 B．乙的产品质量比甲的产品质量好一些

    C．两人的产品质量一样好 D．无法判断谁的质量好一些

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)=(2a1)x ， 若x＞0时总有f(x)＞1，则实数a的取值范围是( )
    A.1＜a＜2
    B.a＜2
    C.a＞1
    D.0<a<1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）求经过直线l1：2x＋3y－5＝0与l2：7x＋15y＋1＝0的交点，且平行于直线x＋2y－3＝0的直线方程;

    （2）求与直线3x＋4y－7＝0垂直，且与原点的距离为6的直线方程．

    查看答案和解析>>

    同步练习册答案