
【题目】已知函数 ![]() 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a和b的值.
(2)说明函数g(x)的单调性;若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围.
(3)设 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
【答案】
(1)解:由g(0)=0得,a=1,
则 ![]() ,
,
经检验g(x)是奇函数,
故a=1,
由f(﹣1)=f(1)得,则 ![]() ,
,
故 ![]() ,
,
经检验f(x)是偶函数
∴a=1, ![]()
(2)解:∵ ![]() ,且g(x)在(﹣∞,+∞)单调递增,且g(x)为奇函数.
,且g(x)在(﹣∞,+∞)单调递增,且g(x)为奇函数.
∴由g(t2﹣2t)+g(2t2﹣k)>0恒成立,
得g(t2﹣2t)>﹣g(2t2﹣k)=g(﹣2t2+k),
∴t2﹣2t>﹣2t2+k,t∈[0,+∞)恒成立
即3t2﹣2t>k,t∈[0,+∞)恒成立
令F(x)=3t2﹣2t,在[0,+∞)的最小值为 ![]()
∴ ![]()
(3)解:h(x)=lg(10x+1),
h(lg(10a+9))=lg[10lg(10a+9)+1]=lg(10a+10)
则由已知得,存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,
而g(x)在(﹣∞,1]单增,
∴ ![]()
∴ ![]()
∴ ![]()
又 ![]()
又∵ ![]()
∴ ![]()
∴ ![]()
【解析】(1)由函数 ![]() 是奇函数,f(x)=lg(10x+1)+bx是偶函数,可得g(0)=0,f(﹣1)=f(1),进而可得a和b的值.(2)g(x)在(﹣∞,+∞)单调递增,且g(x)为奇函数.若g(t2﹣2t)+g(2t2﹣k)>0恒成立,则3t2﹣2t>k,t∈[0,+∞)恒成立,令F(x)=3t2﹣2t,求其最值,可得答案;(3)h(x)=lg(10x+1),若存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,则
是奇函数,f(x)=lg(10x+1)+bx是偶函数,可得g(0)=0,f(﹣1)=f(1),进而可得a和b的值.(2)g(x)在(﹣∞,+∞)单调递增,且g(x)为奇函数.若g(t2﹣2t)+g(2t2﹣k)>0恒成立,则3t2﹣2t>k,t∈[0,+∞)恒成立,令F(x)=3t2﹣2t,求其最值,可得答案;(3)h(x)=lg(10x+1),若存在x∈(﹣∞,1],使不等式g(x)>lg(10a+10)成立,则 ![]() ,解得答案.
,解得答案.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数奇偶性的性质的理解,了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为15.
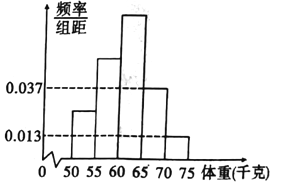
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设![]() 表示体重超过65公斤的学生人数,求
表示体重超过65公斤的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最大值4和最小值1.设
上有最大值4和最小值1.设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其它费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其它费用为每小时1250元.
(1)请把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (海里/小时)的函数,并指明定义域;
(海里/小时)的函数,并指明定义域;
(2)为使全程运输成本最小,轮船应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅲ)在(Ⅰ)的条件下,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com