
【题目】如图2,四边形![]() 为矩形,
为矩形, ![]() ⊥平面
⊥平面![]() ,
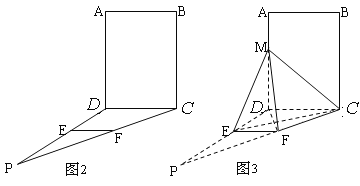
, ![]() ,作如图3折叠,折痕
,作如图3折叠,折痕![]()
![]()
![]() ,其中点
,其中点![]() 分别在线段
分别在线段![]() 上,沿
上,沿![]() 折叠后点
折叠后点![]() 叠在线段
叠在线段![]() 上的点记为
上的点记为![]() ,并且
,并且![]() ⊥
⊥![]() .(1)证明:
.(1)证明: ![]() ⊥平面
⊥平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)要证CF⊥平面MDF,只需证CF⊥MD,且CF⊥MF即可;由PD⊥平面ABCD,得出平面PCD⊥平面ABCD,即证MD⊥平面PCD,得CF⊥MD;(2)求出△CDE的面积S△CDE,对应三棱锥的高MD,计算它的体积VM-CDE.
试题解析:(1)证明:∵PD⊥平面ABCD,PD平面PCD,
∴平面PCD⊥平面ABCD;
又平面PCD∩平面ABCD=CD,MD平面ABCD,MD⊥CD,
∴MD⊥平面PCD,CF平面PCD,∴CF⊥MD;
又CF⊥MF,MD、MF平面MDF,MD∩MF=M,
∴CF⊥平面MDF;

(2)∵CF⊥平面MDF,∴CF⊥DF,
又易知∠PCD=60°,∴∠CDF=30°,∴CF=![]() CD=
CD=![]() ;
;
∵EF∥DC,∴![]() ,即
,即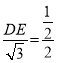 ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() ,
,
![]() =
=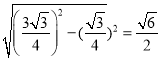 ,
,
∴![]()


科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且离心率为
,且离心率为![]() ,点
,点![]() 为椭圆上一动点,
为椭圆上一动点, ![]() 内切圆面积的最大值为
内切圆面积的最大值为![]() .
.
(1)求椭圆的方程;
(2)设椭圆的左顶点为![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,连接
两点,连接![]() 并延长分别交直线
并延长分别交直线![]() 于
于![]() 两点,以
两点,以![]() 为直径的圆是否恒过定点?若是,请求出定点坐标;若不是,请说明理由.
为直径的圆是否恒过定点?若是,请求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km). 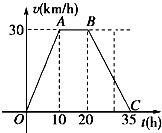
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知10件不同产品中共有4件次品,现对它们进行一一测试,直至找到所有次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品的不同测试方法数有多少种?
(2)若恰在第5次测试后,就找出了所有次品,则这样的不同测试方法数有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上,点A、C为射线PM上的两点,点B、D为射线PN上两点,则有![]() (其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有
(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有![]() =___________.(其中VP-ABE、VP-CDF分别为四面体P-ABE、P-CDF的体积)。
=___________.(其中VP-ABE、VP-CDF分别为四面体P-ABE、P-CDF的体积)。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(x2﹣3)ex , 当m在R上变化时,设关于x的方程f2(x)﹣mf(x)﹣ ![]() =0的不同实数解的个数为n,则n的所有可能的值为( )
=0的不同实数解的个数为n,则n的所有可能的值为( )
A.3
B.1或3
C.3或5
D.1或3或5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 与
与![]() 的中心在原点,焦点分别在
的中心在原点,焦点分别在![]() 轴与
轴与![]() 轴上,它们有相同的离心率
轴上,它们有相同的离心率![]() ,并且
,并且![]() 的短轴为
的短轴为![]() 的长轴,
的长轴,![]() 与
与![]() 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是![]() .
.
(1)求椭圆![]() 与
与![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上非顶点的动点,
上非顶点的动点,![]() 与椭圆
与椭圆![]() 长轴两个顶点
长轴两个顶点![]() ,
,![]() 的连线
的连线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
,![]() 点.
点.
(i)求证:直线![]() ,
,![]() 斜率之积为常数;
斜率之积为常数;
(ii)直线![]() 与直线
与直线![]() 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() =
= ![]() ,
, ![]() =(4sinx,cosx﹣sinx),f(x)=
=(4sinx,cosx﹣sinx),f(x)= ![]()
![]() .
.
(1)求函数f(x)的解析式;
(2)已知常数ω>0,若y=f(ωx)在区间 ![]() 是增函数,求ω的取值范围;
是增函数,求ω的取值范围;
(3)设集合A= ![]() ,B={x||f(x)﹣m|<2},若AB,求实数m的取值范围.
,B={x||f(x)﹣m|<2},若AB,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com