
 的二项展开式前三项的二项式系数和等于79.
的二项展开式前三项的二项式系数和等于79. +2x)12中,令x=1可得其展开式的系数之和;
+2x)12中,令x=1可得其展开式的系数之和; ,代入数据,解可得k=10,即展开式中系数最大的项为T11,计算可得T11的值,即可得答案.
,代入数据,解可得k=10,即展开式中系数最大的项为T11,计算可得T11的值,即可得答案. 的二项展开式的通项为Tr+1=2r•Cnr•(
的二项展开式的通项为Tr+1=2r•Cnr•( )n-r•xr,
)n-r•xr, =79,
=79, +2)12=(
+2)12=( )12,即其展开式的系数之和(
)12,即其展开式的系数之和( )12,
)12, +2x)12=(
+2x)12=( )12(1+4x)12,
)12(1+4x)12,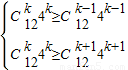
 )12C1210410x10=16896x10.
)12C1210410x10=16896x10.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
| n |  | k=1 |
查看答案和解析>>
科目:高中数学 来源:贵州省遵义四中组团7校2011届高三第一次联考数学理科试题 题型:022
已知(![]() )6的二项展开式中的第5项的值等于5,数列{
)6的二项展开式中的第5项的值等于5,数列{![]() }的前n项为Sn,则
}的前n项为Sn,则![]() ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com