
已知偶函数 在R上的任一取值都有导数,且
在R上的任一取值都有导数,且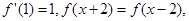 则曲线
则曲线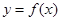 在
在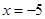 处的切线的斜率为 ( )
处的切线的斜率为 ( )
| A.2 | B.-2 | C.1 | D.-1 |
D
解析试题分析:由f(x)在R上可导,对f(x+2)=f(x-2)两边求导得:
f′(x+2)(x+2)′=f′(x-2)(x-2)′,即f′(x+2)=f′(x-2)①,
由f(x)为偶函数,得到f(-x)=f(x),
故f′(-x)(-x)′=f′(x),即f′(-x)=-f′(x)②,
则f′(x+2+2)=f′(x+2-2),即f′(x+4)=f′(x),
所以f′(-5)=f′(-1)=-f′(1)=-1,即所求切线的斜率为-1.
故选D。
考点:本题主要考查复合函数的导数计算,导数的几何意义。
点评:中档题,本题解答充分借助于已知等式,通过两边求导数,确定得到函数导数值关系,进一步将切线斜率转化成求函数的导数值。


科目:高中数学 来源: 题型:单选题
根据下表中的数据,可以判断函数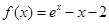 的一个零点所在区间为
的一个零点所在区间为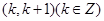 ,则
,则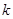 =
=
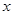 | 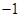 | 0 | 1 | 2 | 3 |
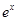 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
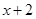 | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
判断下列各组中的两个函数是同一函数的为( )
(1)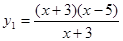 ,
,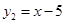 ;
;
(2)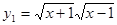 ,
,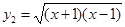 ;
;
(3)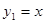 ,
,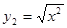 ;
;
(4)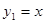 ,
,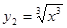 ;
;
(5)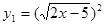 ,
, 。
。
| A.(1),(2) | B.(2),(3) | C.(4) | D.(3),(5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com