
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
分析 求出抛物线的焦点坐标和直线方程,根据双曲线和抛物线的关系求出a,c,解方程求出A,B的坐标进行求解即可.
解答 解:∵抛物线C:y2=8x,
∴抛物线的焦点坐标为(2,0),抛物线的准线方程为x=-2,
则双曲线E的右焦点为(2,0),
则c=2,
∵离心率为2,∴e=$\frac{c}{a}$=2,则a=1,
b2=c2-a2=4-1=3
则双曲线的方程为x2-$\frac{{y}^{2}}{3}$=1,
将x=-2代入x2-$\frac{{y}^{2}}{3}$=1,
得4-$\frac{{y}^{2}}{3}$=1,即$\frac{{y}^{2}}{3}$=3,
则y2=9,y=±3,
即A(-2,3),B(-2,-3)
则|AB|=3-(-3)=6,
故选:B.
点评 本题主要考查双曲线和抛物线性质的应用,根据条件求出双曲线的方程以及交点坐标是解决本题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-$\frac{{\sqrt{2}}}{2}$,1] | D. | [-1,$\frac{{\sqrt{2}}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 中学成绩不优秀 | 中学成绩优秀 | 总计 | |
| 小学成绩优秀 | 5 | 20 | 25 |
| 小学成绩不优秀 | 10 | 5 | 15 |
| 合计 | 15 | 25 | 40 |
| A. | 在犯错误的概率不超过0.1的前提下,认为“小学成绩与中学成绩无关” | |
| B. | 在犯错误的概率不超过0.1的前提下,认为“小学成绩与中学成绩有关” | |
| C. | 在犯错误的概率不超过0.01的前提下,认为“小学成绩与中学成绩无关” | |
| D. | 在犯错误的概率不超过0.01的前提下,认为“小学成绩与中学成绩有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知f(x)=2sin(2x+$\frac{π}{3}$).
已知f(x)=2sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
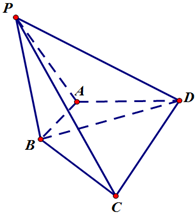 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com