练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （文科）数列{an}的通项公式是a n =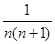(n∈N*)，若前n项的和为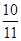，则项数为           

     

    【答案】

    10

    【解析】

    试题分析：.

    考点：裂项求和法求数列的和。

    点评：.根据,可确定求数列{an}的前n项和可采用裂项求和的方法解决。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （文科）数列{ an }中，a1=t，a2=t2，（t≠1）．x=
    		t
    是函数f（x）=an-1x3-3[（t+1）an-an+1]x+1（n≥2）的一个极值点．
    （1）证明数列[an-1-an]是等比数列，并求数列{an}的通项公式；
    （2）记bn=2（1-
    1
    an
    ），当t=2时，数列{bn}的前n项和为Sn，求使Sn＞2010的n的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （文科）数列{an}是首项为21，公差d≠0的等差数列，记前n项和为Sn，若
    1
    10
    S10和
    1
    19
    S19的等比中项为
    1
    16
    S16．数列{bn}满足：bn=anan+1an+2．
    求：（1）数列{an}的通项an；（2）数列{bn}前n项和Tn最大时n的值．

    查看答案和解析>>

    科目：高中数学 来源：2010年江西省名校高考数学信息卷2（文理合卷）（解析版） 题型：解答题

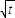    （文科）数列{ an }中，a1=t，a2=t2，（t≠1）．x=是函数f（x）=an-1x3-3[（t+1）an-an+1]x+1（n≥2）的一个极值点．
    （1）证明数列[an-1-an]是等比数列，并求数列{an}的通项公式；
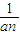    （2）记bn=2（1-），当t=2时，数列{bn}的前n项和为Sn，求使Sn＞2010的n的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2009年湖北省武汉市硚口区高三数学交流试卷1（文理合卷）（解析版） 题型：解答题

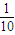    （文科）数列{an}是首项为21，公差d≠0的等差数列，记前n项和为Sn，若S10和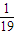S19的等比中项为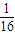S16．数列{bn}满足：bn=anan+1an+2．
    求：（1）数列{an}的通项an；（2）数列{bn}前n项和Tn最大时n的值．

    查看答案和解析>>

    同步练习册答案