
| 1 |
| 2n |
| 1 |
| 2 |
| n |
| 2n+1 |
| n+2 |
| 2n+1 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+2 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2n+1 |
| n+2 |
| 2n+1 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+2 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 23 |
| 4 |
| 24 |
| n+2 |
| 2n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+2 |
| 1 |
| 2 |
| 3 |
| 4 |
| ||||
1-
|
| n+2 |
| 2n+2 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 2n+4 |
| 2n+1 |
| 2n+5 |
| 2n |


科目:高中数学 来源: 题型:
| 4 |
| anan+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PM |
| PN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 蛋白质 | 维生素C | |
| 午餐 | 6 | 6 |
| 晚餐 | 6 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 查验类别 | 甲 | 乙 | ||||
| 所含指标项 | 4 | 2 | ||||
| 每项初查合格率 |
|
| ||||
| 每项复查合格率 |
|
| ||||
| 每项核查合格权重分数 | 2 | 1 | ||||
| 每项核查不合格权重分数 | 0 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
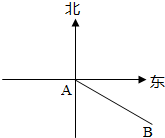 已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.
已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com