
����Ŀ����ƽ��ֱ������ϵxOy�У�������E��x2=4y�Ľ���F����Բ ![]() ��a��b��0����һ�����㣮����F��б��Ϊk��k��0����ֱ��l����ԲC����һ��D����������E��A��B���㣬�߶�DF���е�ΪM��ֱ��OM����ԲC��P��Q���㣬��ֱ��OM��б��Ϊk'������
��a��b��0����һ�����㣮����F��б��Ϊk��k��0����ֱ��l����ԲC����һ��D����������E��A��B���㣬�߶�DF���е�ΪM��ֱ��OM����ԲC��P��Q���㣬��ֱ��OM��б��Ϊk'������ ![]() ��
�� 
��1������ԲC�ķ��̣�
��2���ǡ�PDF�����ΪS1 �� ��QAB�����ΪS2 �� �� ![]() ����ʵ���˵����ֵ��ȡ�����ֵʱֱ��l�ķ��̣�
����ʵ���˵����ֵ��ȡ�����ֵʱֱ��l�ķ��̣�
���𰸡�
��1���⣺���������ֱ��l�ķ���Ϊy=kx+1��
����  ���ã�1+a2k2��x2+2a2kx=0��
���ã�1+a2k2��x2+2a2kx=0��
��ã� ![]() ��
�� ![]() ��
��
��M�� ![]() ��
�� ![]() ������k��=
������k��= ![]() ��
��
�� ![]() ����
���� ![]() ��
��
��a2=4��
����ԲC�ķ���Ϊ ![]()
��2���⣺�ɣ�1����֪��D������Ϊ�� ![]() ������F��0��1����
������F��0��1����
��|DF|= ![]() ��
��
�� ![]() ����x2��4kx��4=0��
����x2��4kx��4=0��
��=16k2+16��0�������
��A��x1��y1����B��x2��y2������x1+x2=4k��x1x2=��4��
��� ![]() =
= ![]() ��
��
�����⣬ֱ��OM�ķ���Ϊy=�� ![]() ��
��
��  ���ã�1+4k2��x2��16k2=0��
���ã�1+4k2��x2��16k2=0��
��Ȼ����=��4��1+4k2������16k2����0���������x= ![]() ��
��
������ ![]() ����
���� ![]() ��
��
���P�������� ![]() ��������Q��������
��������Q�������� ![]() ����
����
��P��ֱ��kx��y+1=0�ľ��� ![]() ��
��
��Q��ֱ��kx��y+1=0�ľ��� ![]() ��
��
�� ![]() =
= ![]() ��
��
![]() =
= ![]() =
= ![]() ��
��
��S1S2= ![]() =
= ![]() ��
��
�� ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
��
���ҽ���3k2=k2+1����k= ![]() ʱ���Ⱥų�����
ʱ���Ⱥų�����
��ʵ���˵����ֵΪ ![]() ����ȡ���ֵʱ��ֱ�߷���Ϊ
����ȡ���ֵʱ��ֱ�߷���Ϊ ![]() ��
��

����������1�����������ֱ��l�ķ���Ϊy=kx+1������Բ�������������D�����꣬�����е����깫ʽ���M�����꣬�õ�OM��б�ʽ����֪���aֵ������Բ���̿���2���ɣ�1����֪��D������Ϊ�� ![]() ������F��0��1�����ɵ�|DF|����
������F��0��1�����ɵ�|DF|���� ![]() �������ҳ���ʽ���|AB|�����ֱ��OM�ķ���Ϊy=��
�������ҳ���ʽ���|AB|�����ֱ��OM�ķ���Ϊy=�� ![]() ����
����  �����P��Q�����꣬�ɵ㵽ֱ�ߵľ��빫ʽ��õ�P��ֱ��kx��y+1=0�ľ���
�����P��Q�����꣬�ɵ㵽ֱ�ߵľ��빫ʽ��õ�P��ֱ��kx��y+1=0�ľ��� ![]() ����Q��ֱ��kx��y+1=0�ľ���
����Q��ֱ��kx��y+1=0�ľ��� ![]() �����������������ʽ�����������û�������ʽ���ʵ���˵����ֵ��ȡ�����ֵʱֱ��l�ķ��̣�
�����������������ʽ�����������û�������ʽ���ʵ���˵����ֵ��ȡ�����ֵʱֱ��l�ķ��̣�


 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABC��A1B1C1�У�AC��AB��AB=2AA1 �� M��AB���е㣬��A1MC1�ǵ��������Σ�DΪCC1���е㣬EΪBC��һ�㣮
������DE��ƽ��A1MC1 �� �� ![]() ��
��
������ֱ��BG��ƽ��A1MC1���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫ263�����ң��ҹ���ѧ�����շ��֣���Բ�ڽӶ���εı�����������ʱ���������������ޱƽ�Բ��������ɴ˴����˸�Բ�������ø�Բ�����յõ���Բ���ʾ�ȷ��С���������λ�Ľ���ֵ3��14������������Ļ��ʣ���ͼ���������յĸ�Բ����Ƶij����ͼ���������nֵΪ�� �� �ο����ݣ� ![]() ��sin15���0.2588��sin7.5���0.1305��
��sin15���0.2588��sin7.5���0.1305��
A.12
B.24
C.48
D.96
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=x ln x��ax2+��2a��1��x��a��R��
������g��x��=f�䣨x ������ g��x���ĵ������䣻
����a��0ʱ��ֱ�� y=t����1��t��0����f��x����ͼ������������A��x1 �� t����B��x2 �� t������x1��x2 �� ��֤��x1+x2��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() ��ͼ����ÿ��ĺ��������̵�ԭ����
��ͼ����ÿ��ĺ��������̵�ԭ���� ![]() ���������겻�䣩���õ�����y=f��x����ͼ��
���������겻�䣩���õ�����y=f��x����ͼ��
��1������f��x���Ľ���ʽ����ͼ��ĶԳ��᷽�̣�
��2���ڡ�ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c���� ![]() ����sinB��ֵ��
����sinB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=4cosxsin��x+ ![]() ��+m��m��R������x��[0��
��+m��m��R������x��[0�� ![]() ]ʱ��f��x������СֵΪ��1��
]ʱ��f��x������СֵΪ��1��
������m��ֵ��
�����ڡ�ABC�У���֪f��C��=1��AC=4���ӳ�AB��D��ʹBC=BD����AD=5�����ACD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫ263�����ң��ҹ���ѧ�����շ��ֵ�Բ�ڽ�������εı�����������ʱ���������������ޱƽ�Բ��������������ˡ���Բ���������á���Բ�������յõ���Բ���ʾ�ȷ��С�������λ�Ľ���ֵ3.14������������ġ����ʡ�����ͼ���������յġ���Բ����˼����Ƶ�һ�������ͼ�������n��ֵΪ�� �� ���ο����ݣ� ![]() ��1.732��sin15���0.2588��sin7.5���0.1305��
��1.732��sin15���0.2588��sin7.5���0.1305��
A.12
B.24
C.36
D.48
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() x2+ax��g��x��=ex �� a��R��a��0��e=2.718����eΪ��Ȼ�����ĵ�����
x2+ax��g��x��=ex �� a��R��a��0��e=2.718����eΪ��Ȼ�����ĵ�����
��������h��x��=f��x��g��x����[��1��1]�ϼ�ֵ��ĸ�����
�������p��x��=f'��x��g��x������a��[1��3]������p��x��������[b+a��ea �� +��]�Ͼ�Ϊ����������֤��b��e3��7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������S��ABCD�У�����ABCD�DZ߳�Ϊ4�����Σ���ABC=60�㣬SA��ƽ��ABCD����SA=4��M����SA�ϣ���AM=1��N����SD����SN=2ND�� ������֤��CN����BDM��
������ֱ��SD��ƽ��BDM���ɵĽǵ�����ֵ��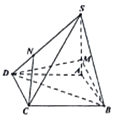
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com