
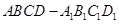 ,的棱长为1,
,的棱长为1,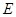 为
为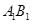 的中点,则下列五个命题:
的中点,则下列五个命题: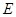 到平面
到平面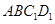 ,的距离为
,的距离为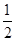
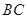 与平面
与平面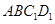 ,所成的角等于
,所成的角等于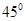
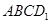 ,在正方体六个面内形成六个射影,其面积的最小值是
,在正方体六个面内形成六个射影,其面积的最小值是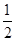
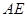 与
与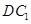 所成的角
所成的角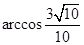
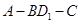 的大小为
的大小为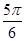
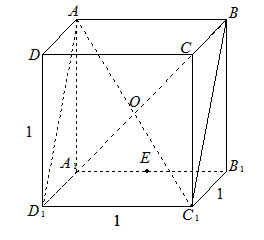
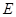 点的一条垂直于面
点的一条垂直于面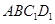 的直线,很简单地我们发现
的直线,很简单地我们发现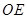 (
(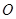 为正方体的中心)是一条符合要求的直线,所以距离为面对角线长的一半即
为正方体的中心)是一条符合要求的直线,所以距离为面对角线长的一半即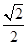 ,假;②考查直线与面的夹角,显然直线
,假;②考查直线与面的夹角,显然直线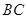 与面
与面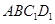 有交点
有交点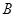 ,再从侧面
,再从侧面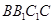 看显然直线与面的夹角为
看显然直线与面的夹角为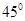 ,真;③考查空间上的面射影,按照射影的规律我们依次得到空间四边形
,真;③考查空间上的面射影,按照射影的规律我们依次得到空间四边形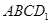 的前后射影、左右射影均为直角边长为1的直角三角形,上下射影为边长为1的正方形,故最小射影的面积为
的前后射影、左右射影均为直角边长为1的直角三角形,上下射影为边长为1的正方形,故最小射影的面积为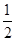 ,真;④考查空间中的直线夹角,显然采取平移的办法将
,真;④考查空间中的直线夹角,显然采取平移的办法将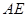 移到面
移到面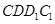 上,则由余弦定理知两直线夹角的余弦值为
上,则由余弦定理知两直线夹角的余弦值为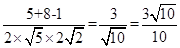 (计算时将边长扩大了一倍计算更为方便)则夹角为
(计算时将边长扩大了一倍计算更为方便)则夹角为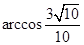 ,真;⑤考查二面角,显然
,真;⑤考查二面角,显然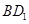 是体对角线,
是体对角线,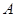 、
、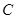 两点关于面
两点关于面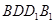 对称,则将问题简化为点
对称,则将问题简化为点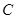 与面
与面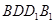 的夹角两倍的求解,再将问题从空间简化到平面
的夹角两倍的求解,再将问题从空间简化到平面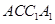 上来,则夹角
上来,则夹角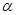 的正切值为
的正切值为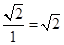 (同样将数据扩大了一倍)则有所求二面角为
(同样将数据扩大了一倍)则有所求二面角为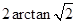 ,不等于
,不等于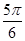 ,假。综上,正确答案是②③④。
,假。综上,正确答案是②③④。

科目:高中数学 来源:不详 题型:解答题
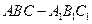 中,侧面
中,侧面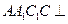 底面ABC,
底面ABC,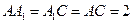 ,
,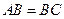 ,且
,且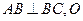 为AC中点。
为AC中点。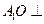 平面ABC;
平面ABC;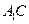 与平面
与平面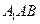 所成角的正弦值;
所成角的正弦值;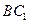 上是否存在一点E,使得
上是否存在一点E,使得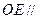 平面
平面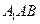 ,若不存在,说明理由;若存在,确定点E的位置。
,若不存在,说明理由;若存在,确定点E的位置。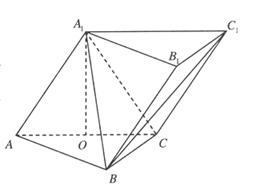
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
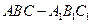 中,每个侧面均为正方形,
中,每个侧面均为正方形,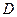 为底边
为底边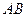 的中点,
的中点,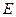 为侧棱
为侧棱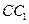 的中点.
的中点.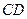 ∥平面
∥平面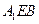 ;
;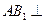 平面
平面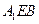 ;
;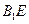 与平面
与平面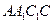 所成角的正弦值.
所成角的正弦值. 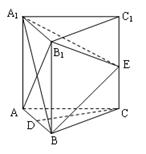
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 底面ABCD,PA=2,
底面ABCD,PA=2,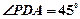 ,
,
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
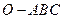 的三条侧棱
的三条侧棱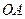 、
、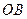 、
、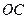 两两垂直,且长度均为2.
两两垂直,且长度均为2.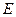 、
、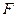 分别是
分别是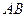 、
、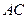 的中点,
的中点,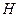 是
是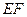 的中点,过
的中点,过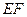 作平面与侧棱
作平面与侧棱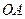 、
、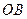 、
、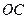 或其延长线分别相交于
或其延长线分别相交于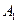 、
、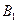 、
、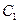 ,已知
,已知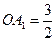 。
。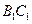 ⊥平面
⊥平面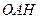 ;
;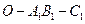 的大小。
的大小。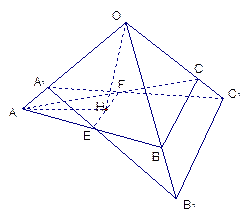
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
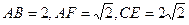 ,CE//AF,
,CE//AF,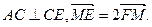
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 E是BC的中点。
E是BC的中点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com