Question

在△ABC中，a，b，c分别为内角A，B，C的对边，

且2asinA=（2b+c）sinB+（2c+b）sinC．

(1)求A的大小；

(2)求sinB+sinC的最大值．

Answer 1

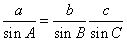（Ⅰ）设=2R
则a=2RsinA，b=2RsinB，c=2RsinC..................................2分
∵2asinA=（2b+c）sinB+（2c+b）sinC
方程两边同乘以2R
∴2a²=（2b+c）b+（2c+b）c..............................................2分
整理得a²=b²+c²+bc.................................................1分
∵由余弦定理得a²=b²+c²-2bccosA.....................................1分
故cosA=-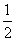，A=120°.........................................2分
（Ⅱ）由（Ⅰ）得：sinB+sinC=sinB+sin（60°-B）...........................1分

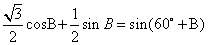=.......................................2分

故当B=30°时，sinB+sinC取得最大值1．.....................1分