
(2010•福建)本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)已知矩阵M=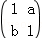 ,
,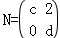 ,且
,且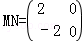 ,
,
(Ⅰ)求实数a,b,c,d的值;
(Ⅱ)求直线y=3x在矩阵M所对应的线性变换下的像的方程.
(2)在直角坐标系xoy中,直线l的参数方程为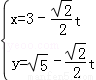 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为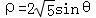 .
.
(Ⅰ)求圆C的直角坐标方程;(Ⅱ)设圆C与直线l交于点A、B,若点P的坐标为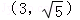 ,
,
求|PA|+|PB|.
(3)已知函数f(x)=|x﹣a|.
(Ⅰ)若不等式f(x)≤3的解集为{x|﹣1≤x≤5},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
见解析
【解析】
试题分析:选作题1:(Ⅰ)由矩阵MN的表达式,把他们相乘使左边等于右边既可求解实数a,b,c,d的值.
(Ⅱ)矩阵M所对应的线性变换将直线变成直线,可选直线y=3x上的两点做矩阵M所对应的线性变换下的像,即可确定原直线的像.
选做题2:(Ⅰ)由极坐标转化为直线坐标方程.
(Ⅱ)将直线的参数方程代入圆的直角坐标系,根据根与系数关系求出两实根的关系式,再有t的几何意义求解.
选做题3:(Ⅰ)首先把函数的参数表达式≤3,解不等式求出a的值.
(Ⅱ)由上题解得的当a=2时,f(x)=|x﹣2|,可设函数g(x)=f(x)+f(x+5),求出g(x)的函数表达式使其≥m对一切实数x恒成立.求解M的范围.
(1)选修1:【解析】
(Ⅰ)由题设得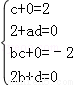 ,解得
,解得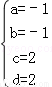 ;
;
(Ⅱ)因为矩阵M所对应的线性变换将直线变成直线(或点),所以可取直线y=3x上的两(0,0),(1,3),
由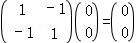 ,
,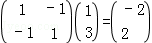 ,
,
得点(0,0),(1,3)在矩阵M所对应的变换下的线的像是(0,0),(﹣2,2),
从而直线y=3x在矩阵M所对应的线性变换下的像的方程为y=﹣x.
(2)选修2:【解析】
(Ⅰ)由ρ=2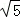 sinθ得x2+y2﹣2
sinθ得x2+y2﹣2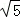 y=0,即
y=0,即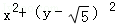 =5.
=5.
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得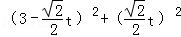 =5,
=5,
即t2﹣3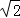 t+4=0,
t+4=0,
由于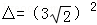 ﹣4×4=2>0,
﹣4×4=2>0,
故可设t1,t2是上述方程的两实根,
所以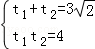 ,
,
又直线l过点P(3,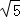 ),
),
故由上式及t的几何意义得:
|PA|+|PB|=|t1|+|t2|=t1+t2=3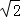 .
.
(3)选修3:【解析】
(Ⅰ)由f(x)≤3得|x﹣a|≤3,解得a﹣3≤x≤a+3,
又已知不等式f(x)≤3的解集为{x|﹣1≤x≤5},
所以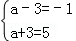 ,解得a=2.
,解得a=2.
(Ⅱ)当a=2时,f(x)=|x﹣2|,
设g(x)=f(x)+f(x+5),
于是g(x)=|x﹣2|+|x+3|=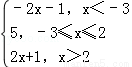 ,
,
所以,当x<﹣3时,g(x)>5;
当﹣3≤x≤2时,g(x)=5;
当x>2时,g(x)>5.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 3.3逆矩阵与二元一次方程组(解析版) 题型:填空题
(2014•黄浦区一模)各项都为正数的无穷等比数列{an},满足a2=m,a4=t,且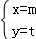 是增广矩阵
是增广矩阵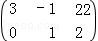 的线性方程组
的线性方程组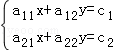 的解,则无穷等比数列{an}各项和的数值是 .
的解,则无穷等比数列{an}各项和的数值是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:选择题
(2013•房山区二模)定义运算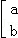
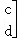
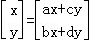 ,称
,称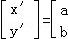
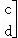
 为将点(x,y)映到点(x′,y′)的一次变换.若
为将点(x,y)映到点(x′,y′)的一次变换.若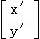 =
=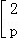
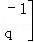
 把直线y=kx上的各点映到这点本身,而把直线y=mx上的各点映到这点关于原点对称的点.则k,m,p,q的值依次是( )
把直线y=kx上的各点映到这点本身,而把直线y=mx上的各点映到这点关于原点对称的点.则k,m,p,q的值依次是( )
A.k=1,m=﹣2,p=3,q=3 B.k=1,m=3,p=3,q=﹣2
C.k=﹣2,m=3,p=3,q=1 D.k=﹣2,m=1,p=3,q=3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
抛物线y2=2px,(p>0)绕焦点依逆时针方向旋转90°所得抛物线方程为( )
A.x2=2py
B.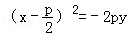
C.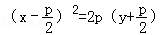
D.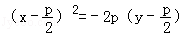
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com