
����Ŀ��ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��1000��ѧ���������ȡ��100��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ.
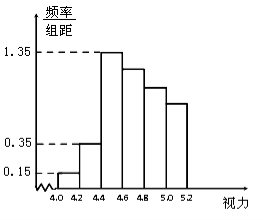
��1����ֱ��ͼ�к������Ƶ���ɵȲ����У��Թ���ȫ�꼶������5.0���µ�������
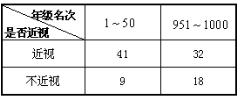
��2��ѧϰС���Ա���֣�ѧϰ�ɼ�ͻ����ѧ�������ӵıȽ϶࣬Ϊ���о�ѧ����������ѧϰ�ɼ��Ƿ��й�ϵ�����꼶������1��50����951��1000����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��3���ڣ�2���е����100��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��9�ˣ���һ�������������õĻ���ϰ�ߣ���������9������ȡ3�ˣ���������1��50��ѧ������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
����

![]()
���𰸡���1��820�ˣ���2���ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ����3���ֲ��м�����������Ϊ1��
��������
�����������1������Ƶ�ʿɼ����ǰ�����Ƶ����Ȼ�����ú�����Ƶ���ɵȲ����пɵú������Ƶ���Ӷ��ó�������������5.0���µ��������ٵó�ȫ�꼶������5.0���µ���������2��������![]() ��ʽ�����
��ʽ�����![]() �����������ݱȽϿɵ�����ԣ���3��������9�����꼶������1��50����951��1000���ֱ���3�˺�6�ˣ�
�����������ݱȽϿɵ�����ԣ���3��������9�����꼶������1��50����951��1000���ֱ���3�˺�6�ˣ�
![]() ��ȡ0��1��2��3���ɹŵ�����ʹ�ʽ�ɼ�������¼����ʣ��ø��ʷֲ��У�����ѧ������ʽ�ɼ����������
��ȡ0��1��2��3���ɹŵ�����ʹ�ʽ�ɼ�������¼����ʣ��ø��ʷֲ��У�����ѧ������ʽ�ɼ����������
�����������1��������Ƶ��Ϊ![]() ��
��
��ͼ��֪����һ����3�ˣ��ڶ���7�ˣ�������27�ˣ�
��Ϊ�������Ƶ���ɵȲ����У�
���Ժ�����Ƶ������Ϊ![]()
����������5.0���µ�Ƶ��Ϊ3+7+27+24+21=82�ˣ�
��ȫ�꼶������5.0���µ�����ԼΪ![]()
��2��![]()
����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ.
��3��������9�����꼶������1��50����951��1000���ֱ���3�˺�6�ˣ�![]() ��ȡ0��1��2��3
��ȡ0��1��2��3
![]() ��
��![]() ��
��
![]() ��
��![]()
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ����ѧ����
����ѧ����![]()


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �������ڶ������е�����
�������ڶ������е�����![]() ������
������![]() ���������ƺ���
���������ƺ���![]() Ϊ�����º�������
Ϊ�����º�������
��1��֤��������![]() �����º�����
�����º�����
��2��������![]() �����º�������ʵ��m��ȡֵ��Χ��
�����º�������ʵ��m��ȡֵ��Χ��
��3�����������ʵ��b������![]() ���������º�������ʵ��c��ȡֵ��Χ��
���������º�������ʵ��c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ʽa2x��1��ax+2��a��0����a��1����x��ȡֵ��Χ���ü��ϱ�ʾ����
��2����֪![]() �Ƕ�����R�ϵ��溯�����ҵ�
�Ƕ�����R�ϵ��溯�����ҵ�![]() ʱ��
ʱ�� ![]() ������
������![]() �Ľ���ʽ.
�Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����շת�������228��1995�����Լ����
��2�����ؾ����㷨�����ʽf��x��=![]() +
+![]() -8x+5��x=2ʱ��ֵ��
-8x+5��x=2ʱ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�е�����Ԥ����,������ˮ����Ԥ����,����Ԥ�������콵ˮ����Ϊ90%��,����ָ(����)
A. ����õ���Լ��90%�ĵط��ήˮ,����ط�����ˮ
B. ����õ���Լ90%��ʱ��ήˮ,����ʱ�䲻��ˮ
C. ����̨��ר����,��90%��Ϊ����ήˮ,�����ר����Ϊ����ˮ
D. ����õ�����ˮ�Ŀ�����Ϊ90%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����pVq�Ǽ����⣬�� ��
A. p��q������һ���Ǽ����� B. p��q ��Ϊ������
C. p��q��ǡ��һ���Ǽ����� D. p��q������һ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ף���죬ij��ѧ��ί��֯������������������л���֪ʶ�������Ӳμӿ��Ե�ѧ���г��60��ѧ��������ɼ����ɼ���Ϊ�������ֳ�����![]() ��
��![]() ������
������![]() ����ͼ�IJ���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
����ͼ�IJ���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺

��1�������С���Ƶ�ʣ�����ȫ���Ƶ�ʷֲ�ֱ��ͼ��
��2��������ο��Եļ�������60�ּ�����Ϊ��������ƽ���֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±���
x | ��3 | ��2 | ��1 | 1 | 2 | 3 |
f��x�� | 5 | 1 | ��1 | ��3 | 3 | 5 |
g��x�� | 1 | 4 | 2 | 3 | ��2 | ��4 |
��f[g��3����f����1��]�� �� ��
A.3
B.4
C.��3
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={2,9},B={m2,2}����A=B,��ʵ��m��ֵΪ �� ��
A.3
B.��3
C.9
D.��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com