【题目】（1）用辗转相除法求228与1995的最大公约数．
（2）用秦九韶算法求多项式f（x）=
+
-8x+5在x=2时的值。
【答案】（1）57（2）101
【解析】
试题分析：（1）用较大的数字除以较小的数字，得到商和余数，然后再用上一式中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约数；（2）首先把一个n次多项式f（x）写成（…（（a[n]x+a[n-1]）x+a[n-2]）x+…+a[1]）x+a[0]的形式，然后化简，求n次多项式f（x）的值就转化为求n个一次多项式的值，求出函数的值
试题解析：（1）解：1995=228
8+171， 228=171
1+57， 171=57
3
因此57是1995与228的最大公约数。
（2）解： f（x）=
+
-8x+5=（（（（3x+0）x+2）x+0）x-8）x+5
=3, 
=3
2=6, 
=6
2+2=14, 
=14
2=28
=28
2-8=48, 
=48
2+5=101
所以，当x=2时，多项式的值是101．
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么y=x2 ， 值域为{1，9}的“同族函数”共有（ ）
A.7个
B.8个
C.9个
D.10个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
,半径为
的圆
与
相切，圆心在
轴上且在直线
的右上方．
（1）求圆的方程；
（2）若直线过点
且与圆
交于
两点（
在
轴上方,B在轴下方），问在
轴正半轴上是否存在定点
,使得轴平分
？若存在，请求出点
的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设a1，d为实数，首项为a1，公差为d的等差数列{an}的前n项和为Sn，满足S5S6＋15＝0．
（1）若S5＝5，求S6及a1；
（2）求d的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图.
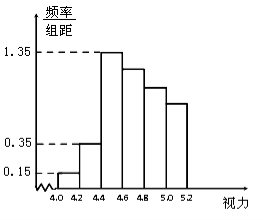
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在5.0以下的人数；
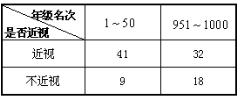
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在1～50名和951～1000名的学生进行了调查，得到右表中数据，根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
（3）在（2）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在1～50的学生人数为
，求的分布列和数学期望.
附：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地空气中出现污染，须喷洒一定量的去污剂进行处理.据测算，每喷洒
个单位的去污剂，空气中释放的浓度
（单位：毫克/立方米）随着时间
单位：天）变化的函数关系式，近似为
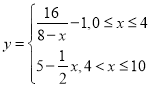,若多次喷洒，则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和. 由实验知，当空气中去污剂的浓度不低于
（毫克/立方米）时，它才能起到去污作用.
（1）若一次喷洒
个单位的去污剂，则去污时间可达几天？
（2）若第一次喷洒
个单位的去污剂，
天后再唢洒
个单位的去污剂，要使接来的
天中能够持续有效去污，试求
的最小值（精确到
，参考数据:
取
）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com