
°æƒø°øƒ≥µÿø’∆¯÷–≥ˆœ÷Œ€»æ£¨–Î≈Á»˜“ª∂®¡øµƒ»•Œ€º¡Ω¯––¥¶¿Ì.æð≤‚À„£¨√ø≈Á»˜![]() ∏ˆµ•Œªµƒ»•Œ€º¡£¨ø’∆¯÷– Õ∑≈µƒ≈®∂»
∏ˆµ•Œªµƒ»•Œ€º¡£¨ø’∆¯÷– Õ∑≈µƒ≈®∂»![]() £®µ•Œª£∫∫¡øÀ/¡¢∑Ω√◊£©ÀÊ◊≈ ±º‰
£®µ•Œª£∫∫¡øÀ/¡¢∑Ω√◊£©ÀÊ◊≈ ±º‰![]() µ•Œª£∫ÃÏ£©±‰ªØµƒ∫Ø ˝πÿœµ Ω£¨Ω¸À∆Œ™
µ•Œª£∫ÃÏ£©±‰ªØµƒ∫Ø ˝πÿœµ Ω£¨Ω¸À∆Œ™
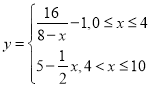 ,»Ù∂ý¥Œ≈Á»˜£¨‘Úƒ≥“ª ±øÃø’∆¯÷–µƒ»•Œ€º¡≈®∂»Œ™√ø¥ŒÕ∂∑≈µƒ»•Œ€º¡‘⁄œý”¶ ±øÃÀ˘ Õ∑≈µƒ≈®∂»÷Æ∫Õ. ”… µ—È÷™£¨µ±ø’∆¯÷–»•Œ€º¡µƒ≈®∂»≤ªµÕ”⁄
,»Ù∂ý¥Œ≈Á»˜£¨‘Úƒ≥“ª ±øÃø’∆¯÷–µƒ»•Œ€º¡≈®∂»Œ™√ø¥ŒÕ∂∑≈µƒ»•Œ€º¡‘⁄œý”¶ ±øÃÀ˘ Õ∑≈µƒ≈®∂»÷Æ∫Õ. ”… µ—È÷™£¨µ±ø’∆¯÷–»•Œ€º¡µƒ≈®∂»≤ªµÕ”⁄![]() £®∫¡øÀ/¡¢∑Ω√◊£© ±£¨À¸≤≈ƒÐ∆µΩ»•Œ€◊˜”√.
£®∫¡øÀ/¡¢∑Ω√◊£© ±£¨À¸≤≈ƒÐ∆µΩ»•Œ€◊˜”√.
£®1£©»Ù“ª¥Œ≈Á»˜![]() ∏ˆµ•Œªµƒ»•Œ€º¡£¨‘Ú»•Œ€ ±º‰ø…¥Ôº∏ÃÏ£ø
∏ˆµ•Œªµƒ»•Œ€º¡£¨‘Ú»•Œ€ ±º‰ø…¥Ôº∏ÃÏ£ø
£®2£©»Ùµ⁄“ª¥Œ≈Á»˜![]() ∏ˆµ•Œªµƒ»•Œ€º¡£¨
∏ˆµ•Œªµƒ»•Œ€º¡£¨![]() ÃÏ∫Û‘ŸþÔ»˜
ÃÏ∫Û‘ŸþÔ»˜![]() ∏ˆµ•Œªµƒ»•Œ€º¡£¨“™ πΩ”¿¥µƒ
∏ˆµ•Œªµƒ»•Œ€º¡£¨“™ πΩ”¿¥µƒ![]() ÃÏ÷–ƒÐπª≥÷–¯”––ß»•Œ€£¨ ‘«Û
ÃÏ÷–ƒÐπª≥÷–¯”––ß»•Œ€£¨ ‘«Û![]() µƒ◊Ó–°÷µ£®æ´»∑µΩ
µƒ◊Ó–°÷µ£®æ´»∑µΩ![]() £¨≤Œøº ˝æð:
£¨≤Œøº ˝æð:![]() »°
»°![]() £©.
£©.
°æ¥∞∏°ø£®1£©![]() £®2£©
£®2£©![]()
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©µ±ø’∆¯÷–»•Œ€º¡µƒ≈®∂»≤ªµÕ”⁄![]() £®∫¡øÀ/¡¢∑Ω√◊£© ±£¨À¸≤≈ƒÐ∆µΩ»•Œ€◊˜”√£¨À˘“‘Ω‚≤ªµ» Ω
£®∫¡øÀ/¡¢∑Ω√◊£© ±£¨À¸≤≈ƒÐ∆µΩ»•Œ€◊˜”√£¨À˘“‘Ω‚≤ªµ» Ω![]() £¨∑÷∂Œ«ÛΩ‚µ√£∫µ±
£¨∑÷∂Œ«ÛΩ‚µ√£∫µ±![]() ±, ¡Ó
±, ¡Ó![]() ,Ω‚µ√
,Ω‚µ√![]() .µ±
.µ±![]() ±, ¡Ó
±, ¡Ó![]() ,Ω‚µ√
,Ω‚µ√![]() .À˘“‘
.À˘“‘ ![]() ,£®2£©µ⁄“ª¥Œ≈Á»˜
,£®2£©µ⁄“ª¥Œ≈Á»˜![]() ∏ˆµ•Œªµƒ»•Œ€º¡£¨
∏ˆµ•Œªµƒ»•Œ€º¡£¨![]() ÃÏ∫Û≈®∂»Œ™
ÃÏ∫Û≈®∂»Œ™![]() £¨‘ŸþÔ»˜
£¨‘ŸþÔ»˜![]() ∏ˆµ•Œªµƒ»•Œ€º¡£¨Ω”¿¥µƒ
∏ˆµ•Œªµƒ»•Œ€º¡£¨Ω”¿¥µƒ![]() ÃÏ÷–≈®∂»Œ™
ÃÏ÷–≈®∂»Œ™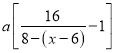 £¨“Ú¥ÀΩ”¿¥µƒ
£¨“Ú¥ÀΩ”¿¥µƒ![]() ÃÏ÷–◊Ð≈®∂»Œ™
ÃÏ÷–◊Ð≈®∂»Œ™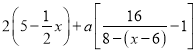 £¨∆‰÷–
£¨∆‰÷–![]() £¨”…“‚“™«Û◊Ð≈®∂»◊Ó–°÷µ≤ª–°”⁄4£¨ø…∏˘æðª˘±æ≤ªµ» Ωµ√◊Ð≈®∂»◊Ó–°÷µŒ™
£¨”…“‚“™«Û◊Ð≈®∂»◊Ó–°÷µ≤ª–°”⁄4£¨ø…∏˘æðª˘±æ≤ªµ» Ωµ√◊Ð≈®∂»◊Ó–°÷µŒ™![]() £¨Ω‚≤ªµ» Ω
£¨Ω‚≤ªµ» Ω![]() £¨º¥ø…µ√
£¨º¥ø…µ√![]() µƒ◊Ó–°÷µŒ™
µƒ◊Ó–°÷µŒ™![]() .
.
‘Ã‚Ω‚Œˆ£∫£®1£©“ÚŒ™“ª¥Œ≈Á»˜![]() ∏ˆµ•Œªµƒ»•Œ€º¡, À˘“‘ø’∆¯÷– Õ∑≈µƒ≈®∂»Œ™
∏ˆµ•Œªµƒ»•Œ€º¡, À˘“‘ø’∆¯÷– Õ∑≈µƒ≈®∂»Œ™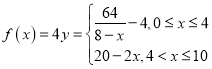 ,
,
µ±![]() ±, ¡Ó
±, ¡Ó![]() ,Ω‚µ√
,Ω‚µ√![]() ,À˘“‘
,À˘“‘![]() .
.
µ±![]() ±, ¡Ó
±, ¡Ó![]() ,Ω‚µ√
,Ω‚µ√![]() ,À˘“‘
,À˘“‘![]() .”⁄ «µ√
.”⁄ «µ√![]() ,º¥“ª¥ŒÕ∂∑≈
,º¥“ª¥ŒÕ∂∑≈![]() ∏ˆµ•Œªµƒ»•Œ€º¡, ”––ß»•Œ€ ±º‰ø…¥Ô
∏ˆµ•Œªµƒ»•Œ€º¡, ”––ß»•Œ€ ±º‰ø…¥Ô![]() ÃÏ.
ÃÏ.
£®2£©…Ë¥”µ⁄“ª¥Œ≈Á»˜∆, æ≠![]() ÃÏ, ≈®∂»
ÃÏ, ≈®∂»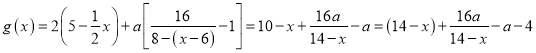 ,
,
“ÚŒ™![]() ,∂¯
,∂¯![]() ,π µ±«“Ωˆµ±
,π µ±«“Ωˆµ±![]() ±,
±,![]() ”–◊Ó–°÷µŒ™
”–◊Ó–°÷µŒ™![]() .
.
¡Ó![]() ,Ω‚µ√
,Ω‚µ√![]() µƒ◊Ó–°÷µŒ™
µƒ◊Ó–°÷µŒ™![]() .
.


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() £¨µ„
£¨µ„![]() «‘≤
«‘≤![]() …œµƒµ„£¨
…œµƒµ„£¨![]() «œþ∂Œ
«œþ∂Œ![]() µƒ÷–µ„£Æ
µƒ÷–µ„£Æ
£®¢Ò£©«Ûµ„![]() µƒπϺ£
µƒπϺ£![]() µƒ∑Ω≥Ã;
µƒ∑Ω≥Ã;
£®¢Ú£©π˝µ„![]() µƒ÷±œþ
µƒ÷±œþ![]() ∫ÕπϺ£
∫ÕπϺ£![]() ”–¡Ω∏ˆΩªµ„
”–¡Ω∏ˆΩªµ„![]() £®
£®![]() ≤ª÷ÿ∫œ£©,»Ù
≤ª÷ÿ∫œ£©,»Ù![]() £¨«Û÷±œþ
£¨«Û÷±œþ![]() µƒ∑Ω≥ãÆ
µƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®1£©”√’∑◊™œý≥˝∑®«Û228”Î1995µƒ◊Ó¥Ûπ´‘º ˝£Æ
£®2£©”√«ÿæ≈…ÿÀ„∑®«Û∂ýœÓ Ωf£®x£©=![]() +
+![]() -8x+5‘⁄x=2 ±µƒ÷µ°£
-8x+5‘⁄x=2 ±µƒ÷µ°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÙpVq «ºŸ√¸Ã‚£¨‘Ú£® £©
A. p£¨q÷¡…Ÿ”–“ª∏ˆ «ºŸ√¸Ã‚ B. p£¨q æ˘Œ™ºŸ√¸Ã‚
C. p£¨q÷–«°”–“ª∏ˆ «ºŸ√¸Ã‚ D. p£¨q÷¡…Ÿ”–“ª∏ˆ «’Ê√¸Ã‚
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™«Ï◊£π˙«Ï£¨ƒ≥÷–—ßÕ≈ŒØ◊È÷Ø¡À°∞∏ËÀÃ◊Êπ˙£¨∞ÆŒ“÷–ª™°±÷™ ∂æ∫»¸£¨¥”≤Œº”øº ‘µƒ—ß…˙÷–≥È≥ˆ60√˚—ß…˙£¨Ω´∆‰≥…º®£®≥…º®æ˘Œ™’˚ ˝£©∑÷≥…¡˘∂Œ![]() £¨
£¨![]() £¨°≠£¨
£¨°≠£¨![]() ∫Ûª≠≥ˆ»ÁÕºµƒ≤ø∑÷∆µ¬ ∑÷≤º÷±∑ΩÕº£¨π€≤ÏÕº–Œµƒ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
∫Ûª≠≥ˆ»ÁÕºµƒ≤ø∑÷∆µ¬ ∑÷≤º÷±∑ΩÕº£¨π€≤ÏÕº–Œµƒ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫

£®1£©«Ûµ⁄Àƒ–°◊ȵƒ∆µ¬ £¨≤¢≤π»´’‚∏ˆ∆µ¬ ∑÷≤º÷±∑ΩÕº£ª
£®2£©π¿º∆’‚¥Œøº ‘µƒº∞∏Ò¬ £®60∑÷º∞“‘…œŒ™º∞∏Ò£©∫Õ∆Ωæ˘∑÷£ª
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµ»—¸»˝Ω«–Œµƒ÷Ð≥§ «18£¨µ◊±þ≥§y «“ª—¸≥§xµƒ∫Ø ˝£¨‘Ú£® £©
A.y£Ω9£≠x£®0£ºx°Ð9£©
B.y£Ω9£≠x£®0£ºx£º9£©
C.y£Ω18£≠2x£®4£Æ5°Ðx°Ð9£©
D.y£Ω18£≠2x£®4£Æ5£ºx£º9£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ€≤Ïœ¬±Ì£∫
x | £≠3 | £≠2 | £≠1 | 1 | 2 | 3 |
f£®x£© | 5 | 1 | £≠1 | £≠3 | 3 | 5 |
g£®x£© | 1 | 4 | 2 | 3 | £≠2 | £≠4 |
‘Úf[g£®3£©£≠f£®£≠1£©]£Ω £® £©
A.3
B.4
C.£≠3
D.5
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø«˙œþf£®x£©=x3+x©Å2‘⁄p0¥¶µƒ«–œþ∆Ω––”⁄÷±œþy=4x©Å1£¨‘Úp0µƒ◊¯±ÍŒ™£® £©
A. £®1£¨0£© B. £®2£¨8£©
C. £®1£¨0£©ªÚ£®©Å1£¨©Å4£© D. £®2£¨8£©ªÚ£®©Å1£¨©Å4£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®±æ–°Ã‚¬˙∑÷12∑÷£©“—÷™Õ÷‘≤![]() ∂Ã÷·µƒ¡Ω∏ˆ∂•µ„”Δ“Ω𵄵ƒ¡¨œþππ≥…µ»±þ»˝Ω«–Œ£¨÷±œþ
∂Ã÷·µƒ¡Ω∏ˆ∂•µ„”Δ“Ω𵄵ƒ¡¨œþππ≥…µ»±þ»˝Ω«–Œ£¨÷±œþ![]() ”Α≤
”Α≤![]() œý«–.
œý«–.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥Ã;
µƒ∑Ω≥Ã;
£®2£©“—÷™Õ÷‘≤![]() µƒ◊Û∂•µ„
µƒ◊Û∂•µ„![]() µƒ¡ΩÃı÷±œþ
µƒ¡ΩÃı÷±œþ![]() ∑÷±ΩªÕ÷‘≤
∑÷±ΩªÕ÷‘≤![]() ”⁄
”⁄![]() ¡Ωµ„,«“
¡Ωµ„,«“![]() ,«Û÷§:÷±œþ
,«Û÷§:÷±œþ![]() π˝∂®µ„,≤¢«Û≥ˆ∂®µ„◊¯±Í£ª
π˝∂®µ„,≤¢«Û≥ˆ∂®µ„◊¯±Í£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬«Û![]() √ʪ˝µƒ◊Ó¥Û÷µ.
√ʪ˝µƒ◊Ó¥Û÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com