练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知点是单位正方体的对角面上的一动点，过点作垂直于平面的直线，与正方体的侧面相交于、两点，则的面积的最大值为（ ）

    A. B. C. D.

    【答案】A

    【解析】

    根据题意和正方体的特征，分析点P动的过程中，x随着y变化情况作出轨迹图象，数形结合能求出结果．

    解：由题意知，MN⊥平面BB1D1D，其轨迹经过B，D1和侧棱AA1，CC1的中点E，F，

    如图，设正方体中心为O1,当P点在线段BO1上运动时，MN随BP的增大而线性增大，所以△BMN的面积表达式应是开口向上的二次函数图像递增的一部分; 当P点在线段D1O1上运动时, MN随D1P的增大而线性减小，所以△BMN的面积表达式应是开口向下的二次函数图像递减的一部分.所以当MN与EF重合时，△BMN的面积取最大值，

    此时，BM＝BN，

    MN，

    S△BMN．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列说法：①若线性回归方程为，则当变量增加一个单位时，一定增加3个单位；②将一组数据中的每个数据都加上同一个常数后，方差不会改变；③线性回归直线方程必过点；④抽签法属于简单随机抽样；其中错误的说法是（ ）

    A.①③B.②③④C.①D.①②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，四边形是菱形，，，且交于点，是上任意一点.

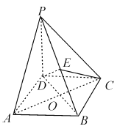
    （1）求证；

    （2）已知二面角的余弦值为，若为的中点，求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线过点，是抛物线上不同两点，且（其中是坐标原点），直线与交于点，线段的中点为.

    （Ⅰ）求抛物线的准线方程；

    （Ⅱ）求证：直线与轴平行.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，点在椭圆上，，分别为椭圆的上、下顶点，点.

    （1）求椭圆的方程；

    （2）若直线与椭圆的另一交点分别为，证明：直线过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋子中有四个小球，分别写有“美、丽、华、一”四个字，有放回地从中任取一个小球，直到“华”“一”两个字都取到就停止，用随机模拟的方法估计恰好在第四次停止的概率．利用计算机随机产生0到3之间取整数值的随机数，分别用0，1，2，3代表“美、丽、华、一”这四个字，以每四个随机数为一组，表示取球四次的结果，经随机模拟产生了以下20组随机数：

    2323 3211 2303 1233 0211 1322 2201 2213 0012 1231

    2312 1300 2331 0312 1223 1031 3020 3223 3301 3212

    由此可以估计，恰好第四次就停止的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，直线的参数方程为（为参数），曲线的参数方程为（为参数），以该直角坐标系的原点为极点，轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （Ⅰ）分别求曲线的极坐标方程和曲线的直角坐标方程；

    （Ⅱ）设直线交曲线于，两点，交曲线于，两点，求的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次公里的自行车个人赛中，25名参赛选手的成绩(单位：分钟)的茎叶图如图所示：

    (1)现将参赛选手按成绩由好到差编为1～25号，再用系统抽样方法从中选取5人，已知选手甲的成绩为85分钟，若甲被选取，求被选取的其余4名选手的成绩的平均数；

    (2)若从总体中选取一个样本，使得该样本的平均水平与总体相同，且样本的方差不大于7，则称选取的样本具有集中代表性，试从总体(25名参赛选手的成绩)选取一个具有集中代表性且样本容量为5的样本，并求该样本的方差.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在几何体中，底面四边形是边长为4的菱形，，，，平面，且，.

    （1）证明：平面平面；

    （2）求三棱锥的体积.

    查看答案和解析>>

    同步练习册答案