【题目】袋子中有四个小球，分别写有“美、丽、华、一”四个字，有放回地从中任取一个小球，直到“华”“一”两个字都取到就停止，用随机模拟的方法估计恰好在第四次停止的概率．利用计算机随机产生0到3之间取整数值的随机数，分别用0，1，2，3代表“美、丽、华、一”这四个字，以每四个随机数为一组，表示取球四次的结果，经随机模拟产生了以下20组随机数：
2323 3211 2303 1233 0211 1322 2201 2213 0012 1231
2312 1300 2331 0312 1223 1031 3020 3223 3301 3212
由此可以估计，恰好第四次就停止的概率为（ ）
A.
B.
C.
D.
科目：高中数学 来源： 题型：
【题目】设曲线
，点
为
的焦点，过点作斜率为1的直线
与曲线交于
，
两点，点，的横坐标的倒数和为-1.
（1）求曲线的标准方程；
（2）过焦点作斜率为
的直线
交曲线于
，
两点，分别以点，为切点作曲线的切线相交于点
，过点作
轴的垂线交轴于点
，求三角形
面积的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设椭圆
(
)的离心率为
，圆
与
轴正半轴交于点
，圆
在点处的切线被椭圆
截得的弦长为
．
(Ⅰ)求椭圆的方程；
(Ⅱ)设圆上任意一点
处的切线交椭圆于点
，试判断
是否为定值？若为定值，求出该定值；若不是定值，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了打好“精准扶贫攻坚战”某村扶贫书记打算带领该村农民种植新品种蔬菜，可选择的种植量有三种：大量种植，适量种植，少量种植．根据收集到的市场信息，得到该地区该品种蔬菜年销量频率分布直方图如图，然后，该扶贫书记同时调查了同类其他地区农民以往在各种情况下的平均收入如表1（表中收入单位：万元）：
表1
销量 种植量 | 好 | 中 | 差 |
大量 |
| 8 | -4 |
适量 | 9 | 7 | 0 |
少量 | 4 | 4 | 2 |
但表格中有一格数据被墨迹污损，好在当时调查的数据频数分布表还在，其中大量种植的100户农民在市场销量好的情况下收入情况如表2：
收入（万元） | 11 | 11.5 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
频数（户） | 5 | 10 | 15 | 10 | 15 | 20 | 10 | 10 | 5 |
（Ⅰ）根据题中所给数据，请估计在市场销量好的情况下，大量种植的农民每户的预期收益．（用以往平均收入来估计）；
（Ⅱ）若该地区年销量在10千吨以下表示销量差，在10千吨至30千吨之间表示销量中，在30千吨以上表示销量好，试根据频率分布直方图计算销量分别为好、中、差的概率（以频率代替概率）；
（Ⅲ）如果你是这位扶贫书记，请根据（Ⅰ）（Ⅱ），从农民预期收益的角度分析，你应该选择哪一种种植量．
查看答案和解析>>
科目：高中数学 来源： 题型：
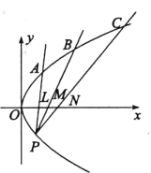
【题目】如图，已知
为抛物线
上在
轴下方的一点，直线
，
，
与抛物线在第一象限的交点从左到右依次为
，
，
，与轴的正半轴分别相交于点
，
，
，且
，直线的方程为
.
（1）当
时，设直线，的斜率分别为
，
，证明：
；
（2）求
关于
的表达式，并求出的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
