
����Ŀ��ij���ε�ij�ֵ���![]() �����������������ٵ��飬����������Ƶ���ֲ������£��������������ݷֳ��ŵ�Ʒ����Ʒ�ʹ�Ʒ���������������������ڻ����
�����������������ٵ��飬����������Ƶ���ֲ������£��������������ݷֳ��ŵ�Ʒ����Ʒ�ʹ�Ʒ���������������������ڻ����![]() ���ĵ������ŵ�Ʒ������С��
���ĵ������ŵ�Ʒ������С��![]() ���ĵ�������Ʒ������ĵ�������Ʒ.
���ĵ�������Ʒ������ĵ�������Ʒ.
���� (��) | Ƶ�� | Ƶ�� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�ϼ� |
|
|
��1������Ƶ�ʷֲ����е����ݣ�д��![]() ��ֵ��
��ֵ��
��2��ij�˴���![]() ������������ع�����
������������ع�����![]() ������˵���ǡ�ò��Ǵ�Ʒ�ĸ��ʣ�
������˵���ǡ�ò��Ǵ�Ʒ�ĸ��ʣ�
��3��ij�˴���������������ع�����![]() ���������
���������![]() �����ݵĵȼ���rǡ���밴�����ȼ��ֲ�������õĽ����ͬ����
�����ݵĵȼ���rǡ���밴�����ȼ��ֲ�������õĽ����ͬ����![]() ����Сֵ.
����Сֵ.
���𰸡���1��![]() ;��2��
;��2��![]() ;��3��10.
;��3��10.
���������������: (1) ��Ƶ�ʷֲ����е����ݣ����![]() ��ֵ��(2)����Ƶ�ʷֲ����е����ݣ�������˹���ĵ������ò��Ǵ�Ʒ�ĸ��ʣ�(3)�������������ŵ�Ʒ����Ʒ�ʹ�Ʒ�ı��������ٰ��ֲ����������������������
��ֵ��(2)����Ƶ�ʷֲ����е����ݣ�������˹���ĵ������ò��Ǵ�Ʒ�ĸ��ʣ�(3)�������������ŵ�Ʒ����Ʒ�ʹ�Ʒ�ı��������ٰ��ֲ����������������������![]() ����Сֵ.
����Сֵ.
�������:��1��![]() .
.
��2���衰���˹���ĵ���ǡ�ò��Ǵ�Ʒ��Ϊ�¼�![]() ���ɱ���֪�������������ŵ�Ʒ��60������Ʒ��100������Ʒ��40�������Դ��˹���ĵ���ǡ�ò��Ǵ�Ʒ�ĸ���Ϊ
���ɱ���֪�������������ŵ�Ʒ��60������Ʒ��100������Ʒ��40�������Դ��˹���ĵ���ǡ�ò��Ǵ�Ʒ�ĸ���Ϊ![]() .
.
��3���ɱ����������������ŵ�Ʒ����Ʒ�ʹ�Ʒ�ı���Ϊ![]() �������ֲ������������ĵ�����
�������ֲ������������ĵ�����![]() ������
������![]() ����СֵΪ10.
����СֵΪ10.


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=cos����x+�գ����أ�0���� ![]() ���գ�0������С������Ϊ�У���f��
���գ�0������С������Ϊ�У���f�� ![]() ��=
��= ![]() ��
�� 
��1����غͦյ�ֵ��
��2���ڸ�������ϵ����������f��x����[0����]�ϵ�ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ����![]() ��
�� ![]() �Dz������Ͷ���
�Dz������Ͷ���![]() �� F1 �� F2 ��Բ���ߵ����ҽ��㣮
�� F1 �� F2 ��Բ���ߵ����ҽ��㣮
��1������ F2 �Ҵ�ֱ��ֱ�� AF1 ��ֱ�� l �IJ������̣�
��2���� P Ϊ���� C �ϵĶ��㣬�� P ��ֱ�� l �����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �͵ȱ�������
�͵ȱ�������![]() �У�
�У� ![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��

��1����![]() ����һ��
����һ��![]() ��ʹ
��ʹ![]() ����˵�����ɣ�
����˵�����ɣ�
��2���ڣ�1���������£���ƽ��![]() ��ƽ��
��ƽ��![]() ��������������ֵ��
��������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��о�ij��ֲ��������ٶ����¶ȵĹ�ϵ������ͳ�ƣ��õ������ٶȣ���λ������/�£�����ƽ�����µĶԱȱ����£�
�¶� | -5 | 0 | 6 | 8 | 12 | 15 | 20 |
�����ٶ� | 2 | 4 | 5 | 6 | 7 | 8 | 10 |
��1���������ٶ�![]() �����¶�
�����¶�![]() �����Իع鷽�̣���б�ʺͽؾ������Ϊ��λ��Ч���֣���
�����Իع鷽�̣���б�ʺͽؾ������Ϊ��λ��Ч���֣���
��2�����ã�1���е����Իع鷽�̣��������´�![]() ��
��![]() ʱ�����ٶȵı仯��������ij�µ�ƽ��������
ʱ�����ٶȵı仯��������ij�µ�ƽ��������![]() ʱ��Ԥ�����´�Լ���������٣�
ʱ��Ԥ�����´�Լ���������٣�
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
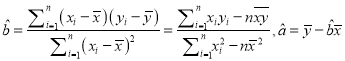 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⳤΪ1��������ABCD��A1B1C1D1�У�E��F�ֱ�Ϊ��AA1��BB1���е㣬GΪ��A1B1�ϵ�һ�㣬��A1G=�ˣ�0�ܦˡ�1�������G��ƽ��D1EF�ľ���Ϊ�� �� 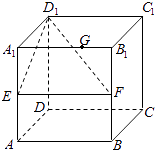
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڱ߳�Ϊ1�ĵȱ�������ABC�У�D��E�ֱ���AB��AC�ϵĵ㣬AD=AE��F��BC���е㣬AF��DE���ڵ�G����ABF��AF���𣬵õ���ͼ2��ʾ������A��BCF������BC= ![]() ��
�� 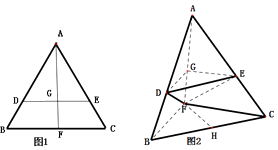
��1����֤��ƽ��DEG��ƽ��BCF��
��2����D��EΪAB��AC�ϵ��е㣬HΪBC�е㣬������ֱ��AB��FH���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P-ABCD�У�����ABCDΪ�����Σ�ƽ��PAD��ƽ��ABCD����M���߶�PPD//ƽ��MAC��PA=PD=![]() ��AB=4��
��AB=4��
��I����֤��MΪPB���е㣻
��II��������B-PD-A�Ĵ�С��
��III����ֱ��MC��ƽ��BDP���ɽǵ�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() x3+ax2��bx��a��b��R������y=f��x��ͼ���ϵĵ㣨1����
x3+ax2��bx��a��b��R������y=f��x��ͼ���ϵĵ㣨1���� ![]() ����������б��Ϊ��4��
����������б��Ϊ��4��
��1����f��x���ı���ʽ��
��2����y=f��x��������[��3��6]�ϵ���ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com