【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中，E、F分别为棱AA1、BB1的中点，G为棱A1B1上的一点，且A1G=λ（0≤λ≤1），则点G到平面D1EF的距离为（ ）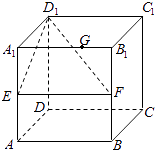 
A.
B.
C.
D.
【答案】D
【解析】解：因为A1B1∥EF，G在A1B1上，所以G到平面D1EF的距离即是A1到面D1EF的距离，
即是A1到D1E的距离，D1E= 
，由三角形面积可得所求距离为 
，
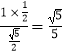故选：D
【考点精析】利用空间点、线、面的位置和空间点、线、面的位置对题目进行判断即可得到答案，需要熟知如果一条直线上的两点在一个平面内，那么这条直线在此平面内;过不在一条直线上的三点，有且只有一个平面;如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线（两个平面的交线）;（平行线的传递性）平行与同一直线的两条直线互相平行；如果一条直线上的两点在一个平面内，那么这条直线在此平面内;过不在一条直线上的三点，有且只有一个平面;如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线（两个平面的交线）;（平行线的传递性）平行与同一直线的两条直线互相平行．
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案科目：高中数学 来源： 题型：
【题目】已知在直角坐标系 
中，圆锥曲线 
的参数方程为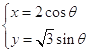 
（ 
为参数），定点 
， 
是圆锥曲线 的左、右焦点．
（1）以坐标原点为极点， 
轴正半轴为极轴建立极坐标系，求经过点 
且平行于直线 
的直线 
的极坐标方程；
（2）设（1）中直线 与圆锥曲线 交于 
两点，求 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）是定义在R上的偶函数，且在（﹣∞，0]上是增函数，设a=f（log47），b=f（log23），c=f（0.20.6），则a，b，c的大小关系是（ ）
A.c＜b＜a
B.b＜c＜a
C.b＜a＜c
D.a＜b＜c
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线 
（ 
为参数）， 
（ 
为参数）．
（1）化 
， 
的方程为普通方程，并说明它们分别表示什么曲线；
（2）若 上的点 
对应的参数为 
， 
为 上的动点，求 
中点 
到直线 
（ 为参数）距离的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某批次的某种灯泡
个，对其寿命进行追踪调查，将结果列成频率分布表如下，根据寿命将灯泡分成优等品、正品和次品三个等级，其中寿命大于或等于
天的灯泡是优等品，寿命小于
天的灯泡是次品，其余的灯泡是正品.
寿命 (天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
（1）根据频率分布表中的数据，写出
的值；
（2）某人从这
个灯泡中随机地购买了
个，求此灯泡恰好不是次品的概率；
（3）某人从这批灯泡中随机地购买了
个，如果这
个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1， 在直角梯形
中， 
， 
， 
， 
为线段
的中点. 将
沿
折起，使平面
平面
，得到几何体
，如图2所示.
（1）求证: 
平面
；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是某校举行歌唱比赛时，七位评委为某位选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的中位数和平均数依次为（ ） 
A.87，86
B.83，85
C.88，85
D.82，86
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
和
是两个等差数列，记
，
其中
表示
这
个数中最大的数．
（Ⅰ）若
， 
，求
的值，并证明
是等差数列；
（Ⅱ）证明：或者对任意正数
，存在正整数
，当
时， 
；或者存在正整数
，使得
是等差数列．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
