
【题目】定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[﹣3,﹣2]时,f(x)=﹣x﹣2,则( )
A.![]() B.f(sin3)<f(cos3)
B.f(sin3)<f(cos3)
C.![]() D.f(2020)>f(2019)
D.f(2020)>f(2019)
科目:高中数学 来源: 题型:
【题目】某工厂的机器上有一种易损元件A,这种元件在使用过程中发生损坏时,需要送维修处维修.工厂规定当日损坏的元件A在次日早上 8:30 之前送到维修处,并要求维修人员当日必须完成所有损坏元件A的维修工作.每个工人独立维修A元件需要时间相同.维修处记录了某月从1日到20日每天维修元件A的个数,具体数据如下表:
日期 | 1 日 | 2 日 | 3 日 | 4 日 | 5 日 | 6 日 | 7 日 | 8 日 | 9 日 | 10 日 |
元件A个数 | 9 | 15 | 12 | 18 | 12 | 18 | 9 | 9 | 24 | 12 |
日期 | 11 日 | 12 日 | 13 日 | 14 日 | 15 日 | 16 日 | 17 日 | 18 日 | 19 日 | 20 日 |
元件A个数 | 12 | 24 | 15 | 15 | 15 | 12 | 15 | 15 | 15 | 24 |
从这20天中随机选取一天,随机变量X表示在维修处该天元件A的维修个数.
(Ⅰ)求X的分布列与数学期望;
(Ⅱ)若a,b![]() ,且b-a=6,求
,且b-a=6,求![]() 最大值;
最大值;
(Ⅲ)目前维修处有两名工人从事维修工作,为使每个维修工人每天维修元件A的个数的数学期望不超过4个,至少需要增加几名维修工人?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(x>0).
,(x>0).
(1)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb](m≠0),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴的正半轴的交点是
轴的正半轴的交点是![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .
.

(1)若直线![]() 与
与![]() 轴交于
轴交于![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的中点为
的中点为![]() ,点
,点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,E是棱
中,E是棱![]() 的中点,F是侧面
的中点,F是侧面![]() 内的动点,且
内的动点,且![]() 与平面
与平面![]() 的垂线垂直,如图所示,下列说法不正确的是( )
的垂线垂直,如图所示,下列说法不正确的是( )
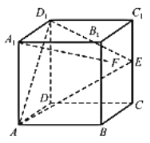
A.点F的轨迹是一条线段B.![]() 与BE是异面直线
与BE是异面直线
C.![]() 与
与![]() 不可能平行D.三棱锥
不可能平行D.三棱锥![]() 的体积为定值
的体积为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com