
【题目】已知函数![]() ,(x>0).
,(x>0).
(1)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb](m≠0),求m的取值范围.
【答案】(1)证明见详解;(2)不存在适合条件的实数a,b,证明见详解;(3)![]() .
.
【解析】
(1)根据函数单调性,初步判断![]() 与1的大小关系,根据f(a)=f(b)得到
与1的大小关系,根据f(a)=f(b)得到![]() 等量关系,用均值不等式进行处理;
等量关系,用均值不等式进行处理;
(2)对![]() 与1的大小关系进行分类讨论,寻找满足题意的
与1的大小关系进行分类讨论,寻找满足题意的![]() ;
;
(3)对![]() 的取值进行分类讨论,利用函数的单调性,进行求解.
的取值进行分类讨论,利用函数的单调性,进行求解.
(1)证明:∵x>0,∴
∴f(x)在(0,1)上为减函数,在(1,+∞)上是增函数.
由0<a<b,且f(a)=f(b),
可得 0<a<1<b和![]() ,
,
即![]() .
.
∴2ab=a+b![]() .
.
故![]() ,即ab>1.
,即ab>1.
(2)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y![]() 的定义域、值域都是[a,b],
的定义域、值域都是[a,b],
则a>0,
①当a,b∈(0,1)时,![]() 在(0,1)上为减函数.
在(0,1)上为减函数.
故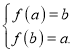 ,即
,即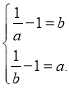 ,解得a=b.
,解得a=b.
故此时不存在适合条件的实数a,b.
②当a,b∈[1,+∞)时,![]() 在(1,+∞)上是增函数.
在(1,+∞)上是增函数.
故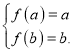 ,即
,即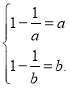
此时a,b是方程x2﹣x+1=0的根,此方程无实根.
故此时不存在适合条件的实数a,b.
③当a∈(0,1),b∈[1,+∞)时,
由于1∈[a,b],而f(1)=0[a,b],
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.
(3)若存在实数a,b(a<b),
使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
①当a,b∈(0,1)时,由于f(x)在(0,1)上是减函数,
故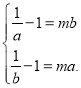 .
.
此时得a,b异号,不符合题意,所以a,b不存在.
②当a∈(0,1)或b∈[1,+∞)时,
由( 2)知0在值域内,值域不可能是[ma,mb]所以a,b不存在.
故只有a,b∈[1,+∞).
∵![]() 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,
∴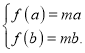 ,即
,即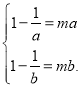
∴a,b是方程mx2﹣x+1=0的两个根,
即关于x的方程mx2﹣x+1=0有两个大于1的实根.
设这两个根为x1,x2,则x1+x2![]() ,x1x2
,x1x2![]() .
.
∴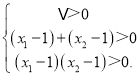 ,即
,即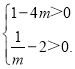
解得![]() .
.
故m的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若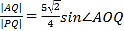 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解广大学生家长对校园食品安全的认识,某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查,每一位学生家长仅有一次参加机会,现对有效问卷进行整理,并随机抽取出了200份答卷,统计这些答卷的得分(满分:100分)制出的频率分布直方图如图所示,由频率分布直方图可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
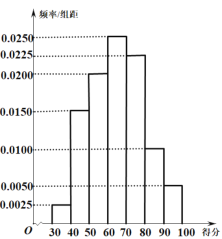
(1)请利用正态分布的知识求![]() ;
;
(2)该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费:
的可以获赠1次随机话费:
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) |
|
|
概率 |
|
|
市食品安全检测部门预计参加此次活动的家长约5000人,请依据以上数据估计此次活动可能赠送出多少话费?
附:①![]() ;②若
;②若![]() ;则
;则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间.
的单调区间.
(2)设直线![]() 是曲线
是曲线![]() 的切线,若
的切线,若![]() 的斜率存在最小值-2,求
的斜率存在最小值-2,求![]() 的值,并求取得最小斜率时切线
的值,并求取得最小斜率时切线![]() 的方程.
的方程.
(3)已知![]() 分别在
分别在![]() ,
,![]() 处取得极值,求证:
处取得极值,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[﹣3,﹣2]时,f(x)=﹣x﹣2,则( )
A.![]() B.f(sin3)<f(cos3)
B.f(sin3)<f(cos3)
C.![]() D.f(2020)>f(2019)
D.f(2020)>f(2019)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com