
分析 (1)求导数,利用曲线y=f(x)在点(1,f(1))处的切线过点(0,-2e),建立方程,即可求a的值;
(2)令h(x)=x(f(x)-g(x))=$\frac{1}{2}{x}^{2}-(a+e)x+aelnx$,则方程f(x)-g(x)=0在区间[$\frac{1}{e}$,+∞)上有且只有两个实数根,等价于函数h(x)在区间[$\frac{1}{e}$,+∞)上有且只有两个零点,分类讨论,确定函数的单调性,即可求a的取值范围.
解答 解:(1)∵f(x)=$\frac{aelnx}{x}$,
∴f′(x)=$\frac{ae(1-lnx)}{{x}^{2}}$,
∴f′(1)=ae,
∵f(1)=0,
∴ae=$\frac{0-(-2e)}{1-0}$=2e,
∴a=2;
(2)令h(x)=x(f(x)-g(x))=$\frac{1}{2}{x}^{2}-(a+e)x+aelnx$,则方程f(x)-g(x)=0在区间[$\frac{1}{e}$,+∞)上有且只有两个实数根,等价于函数h(x)在区间[$\frac{1}{e}$,+∞)上有且只有两个零点,
由h(x)=x(f(x)-g(x))=$\frac{1}{2}{x}^{2}-(a+e)x+aelnx$,可得h′(x)=$\frac{(x-a)(x-e)}{x}$.
①a≤$\frac{1}{e}$,由h′(x)>0,可得x>e,函数单调递增,h′(x)<0,可得$\frac{1}{e}$<x<e,函数单调递减,
∵h(e)=-$\frac{1}{2}{e}^{2}$<0,h(e2)=$\frac{1}{2}e(e-2)({e}^{2}-2a)$≥$\frac{1}{2}e(e-2)({e}^{2}-\frac{2}{e})$>0,
∴要使得h(x)在区间[$\frac{1}{e}$,+∞)上有且只有两个零点,
只需要$h(\frac{1}{e})=\frac{(1-2{e}^{2})-2e(1+{e}^{2})a}{2{e}^{2}}$≥0,
∴a≤$\frac{1-2{e}^{2}}{2e(1+{e}^{2})}$;
②$\frac{1}{e}$<a<e,由h′(x)>0,可得$\frac{1}{e}$<x<a或x>e,函数单调递增,h′(x)<0,可得a<x<e,函数单调递减,
∵h(a)=-$\frac{1}{2}{a}^{2}$<0,h(x)在区间[$\frac{1}{e}$,+∞)上至多只有一个零点,不合题意;
③a>e,由h′(x)>0,可得$\frac{1}{e}$<x<e或x>a,函数单调递增,h′(x)<0,可得e<x<a,函数单调递减,
∵h(e)=-$\frac{1}{2}{e}^{2}$<0,
∴h(x)在区间[$\frac{1}{e}$,+∞)上至多只有一个零点,不合题意;
④a=e,h′(x)≥0,函数单调递增,h(x)在区间[$\frac{1}{e}$,+∞)上至多只有一个零点,不合题意;
综上所述,a≤$\frac{1-2{e}^{2}}{2e(1+{e}^{2})}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查分类讨论的数学思想,属于中档题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
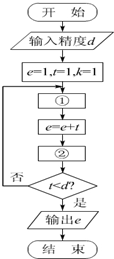 用e≈1+$\frac{1}{1!}$+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{n!}$求e的近似值(n!=1×2×3×…×n),流程图如图所示.在①、②处分别填上适当的式子.①$t=\frac{t}{k}$,②k=k+1.
用e≈1+$\frac{1}{1!}$+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{n!}$求e的近似值(n!=1×2×3×…×n),流程图如图所示.在①、②处分别填上适当的式子.①$t=\frac{t}{k}$,②k=k+1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008×1009 | B. | 1007×1008 | C. | 1005×1004 | D. | 1006×1005 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | $(-∞,\frac{3}{2})$ | D. | $(-∞,\frac{3}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤2016 | B. | a>2016 | C. | a≤2015 | D. | a>2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com