Question

甲、乙、丙三名射击运动员射中目标的概率分别为、a、a(0＜a＜1)，三人各射击一次，击中目标的次数记为ξ.

(1)求ξ的分布列及数学期望；

(2)在概率P(ξ＝i)(i＝0、1、2、3)中，若P(ξ＝1)的值最大，求实数a的取值范围．

 

Answer 1

（1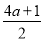），ξ的分布列为

ξ	0	1	2	3
P	(1－a)2	(1－a2)	(2a－a2)

（2）

【解析】(1)P(ξ)是“ξ个人命中，3－ξ个人未命中”的概率．其中ξ的可能取值为0、1、2、3.

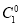
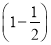
P(ξ＝0)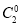＝(1－a)2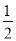＝(1－a)2；

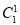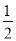
P(ξ＝1)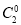＝·(1－a)2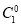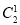＋a(1－a)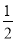＝(1－a2)；

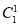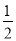
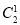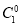
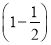
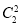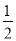P(ξ＝2)＝·a(1－a)＋a2＝(2a－a2)；

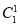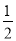
P(ξ＝3)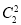＝·a2＝.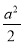

所以ξ的分布列为

 

ξ	0	1	2	3
P	(1－a)2	(1－a2)	(2a－a2)

ξ的数学期望为

E(ξ)＝0×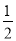(1－a)2＋1×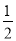(1－a2)＋2×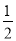(2a－a2)＋3×＝.

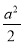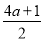(2)P(ξ＝1)－P(ξ＝0)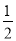＝[(1－a2)－(1－a)2]＝a(1－a)；

P(ξ＝1)－P(ξ＝2)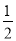＝[(1－a2)－(2a－a2)]＝；

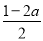P(ξ＝1)－P(ξ＝3)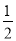＝[(1－a2)－a2]＝.

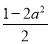由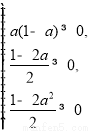和0＜a＜1，得0＜a≤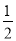，即a的取值范围是.