
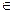 D,使得当x
D,使得当x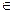 D且x>x0时,总有
D且x>x0时,总有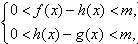 则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=
则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=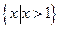 的四组函数如下:
的四组函数如下: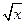 ; ②f(x)=10-x+2,g(x)=
; ②f(x)=10-x+2,g(x)= 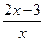 ;
;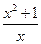 ,g(x)=
,g(x)= 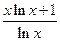 ; ④f(x)=
; ④f(x)= 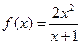 ,g(x)=2(x-1-e-x).
,g(x)=2(x-1-e-x).| A.①④ | B.②③ | C.②④ | D.③④ |
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
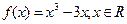 ,又
,又 由
由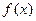 向右平移1个单位,向上平移2个单位得到.
向右平移1个单位,向上平移2个单位得到.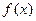 的奇偶性,并求出
的奇偶性,并求出 的极大值与极小值之和.
的极大值与极小值之和.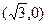 且方向向量为
且方向向量为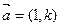 的直线与
的直线与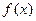 的图像相切,求实数
的图像相切,求实数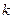 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
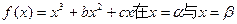 处有两上不同的极值点,设
处有两上不同的极值点,设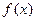 在点
在点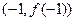 处切线为
处切线为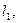 其斜率为
其斜率为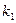 ;在点
;在点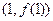 利的切线为
利的切线为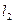 ,其斜率为
,其斜率为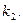
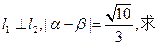
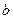 和
和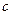 的值
的值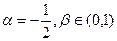 ,求
,求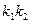 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
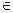 [8,24]元,那么生产哪种档次产品利润最大?
[8,24]元,那么生产哪种档次产品利润最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com