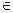练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某产品按质最分成6种不同档次。假设工时不变，每天可生产最低档次40件。若每提高一个档次，每件利润增加1元，但是每天要少生产2件产品。
    (1)若最低档次产品利润每件为16元时，问生产哪种档次产品每天所获利润最大？
    (2)由于原材料价格的浮动，生产最低档次产品每什利润a [8，24]元，那么生产哪种档次产品利润最大？
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    解关于x、y的二元一次方程组，并对解的情况进行讨论.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分12分）
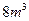    建造一个容积为，深为2m的长方体无盖水池，如果池底的造价为每平方米120元，池壁的造价为每平方米80元，求这个水池的最低造价

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


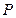    （本小题满分8分）某商品在近30天内每件的销售价格（元）与时间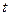天的函数关系是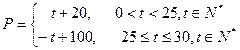该商品的日销售量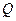（件）与时间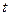（天）的 函数关系是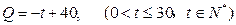（1）,求这种商品的日销售额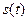的解析式，（2）求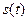的最大值．并指出日销售额的最大时是30天中的第几天

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分：6+8）
    某投资公司投资甲、乙两个项目所得的利润分别是P（亿元）和Q（亿元），它们与投资额t（亿元）的关系有经验公式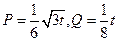，今该公司将5亿元投资这两个项目，其中对甲项目投资x（亿元），投资这两个项目所得的总利润为y（亿元）
    （1）求y关于x的函数表达式；
    （2）求总利润的最大值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    函数f（x）=x4－4x3+10x2，则方程f（x）=0在区间［1，2］上的根有 ___个。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知方程的两根为，并且，则的取值范围是（  ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设是集合到集合的映射，如果，那么等于．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

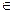    对于具有相同定义域D的函数f（x）和g（x），若存在函数h（x）=kx+b（k,b为常数），对任给的正数m，存在相应的x0D，使得当x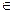D且x>x0时，总有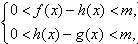则称直线l：y=kx+b为曲线y=f（x）与y=g（x）的“分渐近线”。给出定义域均为D=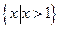的四组函数如下：
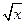    ①f（x）=x2,g(x)= ;    ②f(x)=10-x+2，g(x)= ;
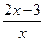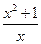    ③f(x)= ,g(x)= 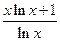;   ④f(x)= 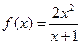，g(x)=2(x-1-e-x).
    其中，曲线y=f(x)与y=g(x)存在“分渐近线”的是
    A．①④B．②③C．②④D．③④

    查看答案和解析>>

    同步练习册答案