
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
 数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,
数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk, )当Φ(x)=2x时 ①求f0(x)和fk
)当Φ(x)=2x时 ①求f0(x)和fk (x)
(x) 的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
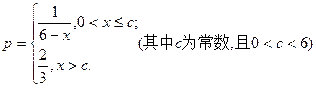 ,每生产1件合格产品盈利3元,每出现1件次品亏损1.5元. (I)将日盈利额y(万元)表示为日产量
,每生产1件合格产品盈利3元,每出现1件次品亏损1.5元. (I)将日盈利额y(万元)表示为日产量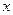 (万件)的函数;(Ⅱ)为使日盈利额最大,日产量应为多少万件?
(万件)的函数;(Ⅱ)为使日盈利额最大,日产量应为多少万件?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
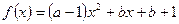 ,其中
,其中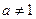 ,若存在实数
,若存在实数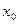 ,使得
,使得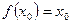 成立,则称
成立,则称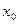 为
为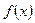 的不动点.
的不动点.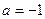 ,
,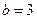 时,求
时,求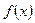 的不动点;
的不动点;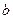 ,函数
,函数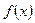 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数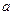 的取值范围;
的取值范围;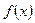 的图像上
的图像上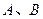 两点的横坐标是函数
两点的横坐标是函数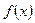 的不动点,且直线
的不动点,且直线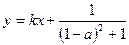 是线段
是线段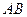 的垂直平分线,求实数
的垂直平分线,求实数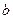 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
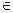 [8,24]元,那么生产哪种档次产品利润最大?
[8,24]元,那么生产哪种档次产品利润最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com