
| A. | M-m=2 | B. | M+m=2 | C. | M-m=4 | D. | M+m=4 |
分析 由题意可得f(x)-1=$\frac{sinx+x}{{6x}^{2}+cosx}$ 为奇函数,它的最大值为M-1,最小值为m-1,由此求得M+m的值.
解答 解:函数f(x)=$\frac{{\sqrt{2}cos({x-\frac{π}{4}})+6{x^2}+x}}{{6{x^2}+cosx}}$=$\frac{{6x}^{2}+cosx+sinx+x}{{6x}^{2}+cosx}$=1+$\frac{sinx+x}{{6x}^{2}+cosx}$,
故f(x)-1=$\frac{sinx+x}{{6x}^{2}+cosx}$ 为奇函数,它的最大值为M-1,最小值为m-1,故M-1+m-1=0;
∴M+m=2,
故选:B.
点评 本题考查了函数的奇偶性的应用,注意化简构造新函数,属于中档题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:解答题
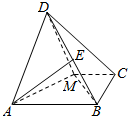 如图,△ADM是等腰直角三角形,AD⊥DM,四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=2,平面ADM⊥平面ABCM.
如图,△ADM是等腰直角三角形,AD⊥DM,四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=2,平面ADM⊥平面ABCM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com