
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | c<b<a |
分析 根据函数的奇偶性得出f(x)=2|x|-1=$\left\{\begin{array}{l}{{2}^{x}-1,x≥0}\\{{2}^{-x}-1,x<0}\end{array}\right.$,利用单调性求解即可.
解答 解:∵定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,
∴f(-x)=f(x),
∴m=0,
∵f(x)=2|x|-1=$\left\{\begin{array}{l}{{2}^{x}-1,x≥0}\\{{2}^{-x}-1,x<0}\end{array}\right.$,
∴f(x)在(0,+∞)单调递增,
∵a=f(log${\;}_{\frac{1}{3}}$4)=f(-log34)=f(log34),b=f(log25),c=f(2m)=f(0)=0,
0<log34<log25,
∴c<a<b,
故选:B.
点评 本题考查了对数函数的性质,函数的奇偶性,单调性,计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | x-2y+4=0 | B. | 3x+4y-18=0 | C. | y+3=0 | D. | x-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
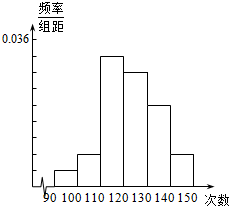 某校抽取一部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为1:2:8:7:5:2,第一小组频数为6.
某校抽取一部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为1:2:8:7:5:2,第一小组频数为6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 4 | C. | $\sqrt{5}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com