
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 利用两个向量数量积的定义求得cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$ 的值,可得θ的值.
解答 解:∵向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,1),设$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为θ,
则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{\sqrt{3}+\sqrt{3}}{2•2}$=$\frac{\sqrt{3}}{2}$,∴θ=30°,
故选:A.
点评 本题主要考查两个向量数量积的定义,根据三角函数的值求角,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\frac{1}{2}})$ | B. | $({-1,\frac{1}{2}})$ | C. | (-∞,-1] | D. | $({-∞,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,6} | B. | {4,5} | C. | {2,4,5} | D. | {2,4,5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.
把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=4x3+x | B. | $f(x)=ln\frac{5-x}{5+x}$ | C. | $f(x)=tan\frac{x}{2}$ | D. | f(x)=ex+e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
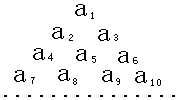 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com