
【题目】已知函数![]() ,
,![]() 为
为![]() 的导数.
的导数.
(1)求![]() 的最值;
的最值;
(2)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)最小值为![]() ,无最大值(2)
,无最大值(2)![]()
【解析】
(1)本题首先可求出![]() 以及
以及![]() ,然后绘出函数
,然后绘出函数![]() 、
、![]() 以及
以及![]() 的图像,结合图像即可得出结果;
的图像,结合图像即可得出结果;
(2)本题首先可判断出函数![]() 是增函数和奇函数,然后根据增函数和奇函数的性质将
是增函数和奇函数,然后根据增函数和奇函数的性质将![]() 转化为
转化为![]() ,最后令
,最后令![]() ,通过求解函数
,通过求解函数![]() 的最值即可得出结果.
的最值即可得出结果.
(1)因为函数![]() ,
,
所以![]() ,
,![]() ,
,
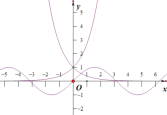
如图,分别绘出函数![]() 、
、![]() 以及
以及![]() 的图像,
的图像,
结合函数图像,易知:
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 取最小值,
取最小值,![]() ,
,
故![]() 有最小值,最小值为
有最小值,最小值为![]() ,无最大值,
,无最大值,
(2)因为![]() ,
,![]()
所以函数![]() 是奇函数,
是奇函数,
因为由(1)可知,![]() ,
,
所以函数![]() 是增函数,
是增函数,
故![]() ,即
,即![]() ,
,![]() ,
,
化简得![]() ,
,
因为![]() 对
对![]() 恒成立,
恒成立,
所以![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,函数
,函数![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,函数
,函数![]() 取最大值,
取最大值,![]() ,
,
因为![]() 恒成立,所以
恒成立,所以![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线的准线与
是抛物线的准线与![]() 轴的交点,直线
轴的交点,直线![]() 经过焦点
经过焦点![]() 且与抛物线相交于
且与抛物线相交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,记
两点,记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() .
.
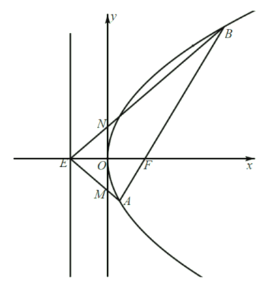
(1)求证: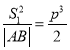 ;
;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,需引进一条新的生产线投入生产,现有两条生产线可供选择,生产线①:有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.01,0.05.若两道工序都没有出现故障,则生产成本为16万元;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.生产线②:有a,b两道独立运行的生产工序,且两道工序出现故障的概率依次是0.04,0.02.若两道工序都没有出现故障,则生产成本为15万元;若a工序出现故障,则生产成本增加8万元;若b工序出现故障,则生产成本增加5万元;若a,b两道工序都出现故障,则生产成本增加13万元.
(1)若选择生产线②,求生产成本恰好为20万元的概率;
(2)为最大限度节约生产成本,你会给工厂建议选择哪条生产线?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,以线段
两点,以线段![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 、
、![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,则( )
,则( )
A.![]()
B.若![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]()
C.若抛物线上存在一点![]() 到焦点
到焦点![]() 的距离等于
的距离等于![]() ,则抛物线的方程为
,则抛物线的方程为![]()
D.若点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() ,则
,则![]() 的最小值为
的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率是( )
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.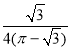
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() 的某一项
的某一项![]() ,若存在
,若存在![]() ,有
,有![]() 成立,则称
成立,则称![]() 具有性质
具有性质![]() .
.
(1)设![]() ,若对任意的
,若对任意的![]() ,
,![]() 都具有性质
都具有性质![]() ,求
,求![]() 的最小值;
的最小值;
(2)设等差数列![]() 的首项
的首项![]() ,公差为
,公差为![]() ,前
,前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 数列
数列![]() 中的项
中的项![]() 都具有性质
都具有性质![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设数列![]() 的首项
的首项![]() ,当
,当![]() 时,存在
时,存在![]() 满足
满足![]() ,且此数列中恰有一项
,且此数列中恰有一项![]() 不具有性质
不具有性质![]() ,求此数列的前
,求此数列的前![]() 项和的最大值和最小值以及取得最值时对应的
项和的最大值和最小值以及取得最值时对应的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区被隔离者是否需要社区非医护人员提供帮助,用简单随机抽样方法从该地区调查了500位被隔离者,结果如下:
性别 是否需要 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区被隔离者中,需要社区非医护人员提供帮助的被隔离者的比例;
(2)能否有99%的把握认为该地区的被隔离者是否需要社区非医护人员提供帮助与性别有关?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com