
若函数 的零点个数为
的零点个数为 ,则
,则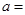 __ __ _
__ __ _
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:填空题
在工程技术中,常用到双曲正弦函数 和双曲余弦函数
和双曲余弦函数 ,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。
,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知两条直线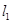 ::y="m" 和
::y="m" 和 :y=
:y= (m>0),直线
(m>0),直线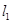 与函数
与函数 的图像从左至右相交于点A,B , 直线
的图像从左至右相交于点A,B , 直线 与函数
与函数 的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a 和b .当m 变化时,
的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a 和b .当m 变化时, 的最小值为 .
的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com