Question

8．已知正方体ABCD-A₁B₁C₁D₁内有一个内切球O，则在正方体ABCD-A₁B₁C₁D₁内任取点M，点M在球O内的概率是（　　）

• A． $\frac{π}{4}$
• B． $\frac{π}{8}$
• C． $\frac{π}{6}$
• D． $\frac{π}{12}$

Answer 1

分析 本题是几何概型问题，欲求点M在球O内的概率，先由正方体ABCD-A1B1C1D1内的内切球O，求出其体积，再根据几何概型概率公式结合正方体的体积的方法易求解．

解答 解：本题是几何概型问题，设正方体的棱长为：2．
正方体ABCD-A₁B₁C₁D₁内的内切球O的半径是其棱长的一倍，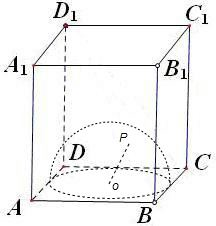

其体积为：V₁=$\frac{4}{3}$π×13=$\frac{4π}{3}$，
则点M在球O内的概率是$\frac{\frac{4π}{3}}{8}$=$\frac{π}{6}$
故选：C．

点评 本小题主要考查几何概型、几何概型的应用、几何体和体积等基础知识，考查空间想象能力、化归与转化思想．属于基中档题．