
分析 (1)总的基本事件数为C93,事件A,可从三类中任取一类,再从该类的3个中任取2个,然后再从其余两类的6个中任取1个,由分步计数原理可得种数,进而可得概率;
(2)①ξ可能的取值为0,1,2,分别求其概率可得分布列;
②易求得期望E(ξ),进而可得E(η),由E(η)>1可得关于λ的不等式,解之可得.
解答 解:(1)当n=3时,即从9个小球中抽取3个,故总的基本事件数为C93,
事件A,可从三类中任取一类共C31种,再从该类的3个中任取2个共C32种,
然后再从其余两类的6个中任取1个共C61种,故总共C31C32C61种,
所以$P(A)=\frac{C_3^1•C_3^2•C_6^1}{C_9^3}=\frac{9}{14}$…4分
(2)①ξ可取0,1,2,则
$P(ξ=0)=\frac{C_6^2}{C_9^3}=\frac{5}{12}$,
$P(ξ=1)=\frac{C_3^1•C_6^1}{C_9^3}=\frac{1}{2}$,
$P(ξ=2)=\frac{C_3^2}{C_9^3}=\frac{1}{12}$…7分
分布列为
| ξ | 0 | 1 | 2 |
| P | $\frac{5}{12}$ | $\frac{1}{2}$ | $\frac{1}{12}$ |
点评 本题考查离散型随即变量及其分布列,涉及数学期望的求解,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
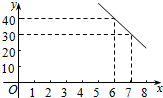 某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2015) | B. | (1,2015) | C. | (2,2014) | D. | (1,2014) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{8}$,-$\frac{1}{8}$) | B. | (-$\frac{3}{8}$,$\frac{1}{8}$) | C. | ($\frac{3}{10}$,-$\frac{1}{10}$) | D. | ($\frac{3}{10}$,$\frac{1}{10}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015+2016i | B. | 2015-2016i | C. | -2016+2015i | D. | -2016-2015i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com