
·ÖÎö £¨1£©ÓÉ̉ÑÖª¿ÉµĂ$\overrightarrow{a}¡Î\overrightarrow{b}$Ç̉·½Ị̈Ïàͬ£¬È»ºóÖ±½ÓÓÉÊưÁ¿»ư¹«Ê½ÇóÖµ£»
£¨2£©ÓÉ̉ÑÖªÇó³ö$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}$£¬¿ª·½µĂ´đ°¸£»
£¨3£©$\overrightarrow a-\overrightarrow b$Óë$\overrightarrow a$´¹Ö±£¬¿ÉµĂ${\overrightarrow{a}}^{2}=\overrightarrow{a}•\overrightarrow{b}=1$£¬ÔÙÓÉÊưÁ¿»ưÇó¼Đ½Ç¹«Ê½ÇóµĂ$\overrightarrow a$Óë$\overrightarrow b$µÄ¼Đ½Ç£®
½â´đ ½â£º£¨1£©¡ß$\sqrt{2}$$\overrightarrow a=\overrightarrow b$£¬¡à$\overrightarrow{a}¡Î\overrightarrow{b}$Ç̉·½Ị̈Ïàͬ£¬̣̉´Ë$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|•cos0=\sqrt{2}$£»
£¨2£©¡ß$\overrightarrow a$Óë$\overrightarrow b$µÄ¼Đ½ÇΪ60¡ă£¬¡à$\overrightarrow{a}•\overrightarrow{b}=1¡Á\sqrt{2}¡Ácos60¡ă=\frac{\sqrt{2}}{2}$£¬
$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}={\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=1+\sqrt{2}+2$=$3+\sqrt{2}$£¬̣̉´Ë$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{3+\sqrt{2}}$£»
£¨3£©¡ß$\overrightarrow a-\overrightarrow b$Óë$\overrightarrow a$´¹Ö±£¬¡à$£¨\overrightarrow{a}-\overrightarrow{b}£©•\overrightarrow{a}=0$£¬ƠûÀíµĂ${\overrightarrow{a}}^{2}=\overrightarrow{a}•\overrightarrow{b}=1$£¬
Áî$\overrightarrow{a}$Óë$\overrightarrow{b}$µÄ¼Đ½ÇΪ¦È£¬̣̉´Ëcos¦È=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}=\frac{1}{1•\sqrt{2}}=\frac{\sqrt{2}}{2}$£¬¡à$\overrightarrow a$Óë$\overrightarrow b$µÄ¼Đ½Ç$¦È=\frac{¦Đ}{4}$£®
µăÆÀ ±¾̀⿼²éƽĂæỊ̈Á¿µÄÊưÁ¿»ưÔËËă£¬¿¼²éÊưÁ¿»ưÇóỊ̈Á¿µÄ¼Đ½Ç£¬ÊÇÖеµ̀⣮


 ÔĶÁ¿́³µÏµÁĐ´đ°¸
ÔĶÁ¿́³µÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | £¨2£¬+¡̃£© | B£® | £¨-¡̃£¬0£© | C£® | £¨4£¬+¡̃£© | D£® | £¨-¡̃£¬-2£© |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | $\frac{9}{5}$ | B£® | 1 | C£® | $-\frac{3}{5}$ | D£® | 0 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | -7 | B£® | -10 | C£® | -8 | D£® | -9 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
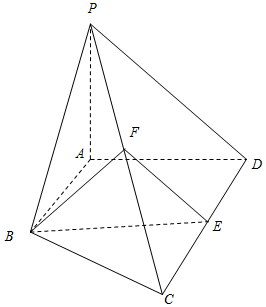 Èçͼ£¬ÔÚËÄÀâ׶P-ABCDÖĐ£¬AB¡ÎCD£¬CD=2AB£¬Æ½ĂæPAD¡Íµ×ĂæABCD£¬PA¡ÍAD£¬EºÍF·Ö±đÊÇCDºÍPCµÄÖĐµă£®
Èçͼ£¬ÔÚËÄÀâ׶P-ABCDÖĐ£¬AB¡ÎCD£¬CD=2AB£¬Æ½ĂæPAD¡Íµ×ĂæABCD£¬PA¡ÍAD£¬EºÍF·Ö±đÊÇCDºÍPCµÄÖĐµă£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | $\frac{5}{2}£¨{2}^{n}-1£©$ | B£® | $\frac{5}{18}£¨{3}^{n}-1£©$ | C£® | $5•{2}^{n-1}-\frac{5}{4}$ | D£® | $5•{2}^{n-2}-\frac{5}{4}$ |
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com