
已知数列{an}中,a1=1,an+1= (n∈N*).
(n∈N*).
(1)求数列{an}的通项an;
(2)若数列{bn}满足bn=(3n-1) an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题6第2课时练习卷(解析版) 题型:选择题
签盒中有编号为1、2、3、4、5、6的六支签,从中任意取3支,设X为这3支签的号码之中最大的一个,则X的数学期望为( )
A.5 B.5.25 C.5.8 D.4.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第1课时练习卷(解析版) 题型:选择题
已知直线l1:k1x+y+1=0与直线l2:k2x+y-1=0,那么“k1=k2”是“l1∥l2”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:解答题
如图,四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.

(1)求证:BC⊥AD;
(2)试问该四面体的体积是否存在最大值?若存在,求出这个最大值及此时棱长AD的大小;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:选择题
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
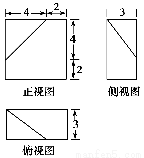
A.108 cm3 B.100 cm3 C.92 cm3 D.84 cm3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:解答题
设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是a和an的等差中项.
(1)证明数列{an}为等差数列,并求数列{an}的通项公式;
(2)证明 <2.
<2.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:选择题
设等差数列{an}的前n项和为Sn,若a11-a8=3,S11-S8=3,则使an>0的最小正整数n的值是( )
A.8 B.9
C.10 D.11
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(解析版) 题型:解答题
已知函数f(x)=2 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为 ,且点
,且点 是它的一个对称中心.
是它的一个对称中心.
(1)求f(x)的表达式;
(2)若f(ax)(a>0)在 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:选择题
设函数f(x)=sin  +sin
+sin  (ω>0)的最小正周期为π,则( )
(ω>0)的最小正周期为π,则( )
A.f(x)在 上单调递减 B.f(x)在
上单调递减 B.f(x)在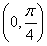 上单调递增
上单调递增
C.f(x)在 上单调递增 D.f(x)在
上单调递增 D.f(x)在 上单调递减
上单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com