
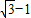 ,BC=
,BC=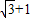 ,
,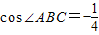 ,且△ACD的面积等于△ABC面积的3倍,求:
,且△ACD的面积等于△ABC面积的3倍,求: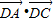 的值;
的值;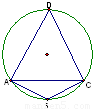
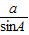 =
=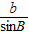 =
=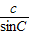 =2R,根据本题的已知条件,可知用正弦定理相对可行,故可由余弦定理求出AC,再由正弦定理求R.
=2R,根据本题的已知条件,可知用正弦定理相对可行,故可由余弦定理求出AC,再由正弦定理求R.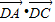 ,根据向量数量积的计算公式,我们要求出两个向量模的积及夹角的余弦值,由∠B与∠D互补,夹角的余弦值易得,然后根据△ACD的面积等于△ABC面积的3倍,也可以得到两个向量模的积,代入可得答案.
,根据向量数量积的计算公式,我们要求出两个向量模的积及夹角的余弦值,由∠B与∠D互补,夹角的余弦值易得,然后根据△ACD的面积等于△ABC面积的3倍,也可以得到两个向量模的积,代入可得答案.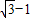 ,BC=
,BC=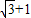 ,我们要求四边形的周长,关键是要求出AD、CD边的长,结合(2)结论和余弦定理,易得答案.
,我们要求四边形的周长,关键是要求出AD、CD边的长,结合(2)结论和余弦定理,易得答案.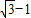 ,BC=
,BC=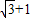 ,
,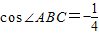 ,
,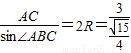 ,
,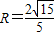 ;
; ,
,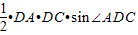 =
=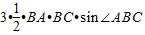
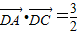 ;
;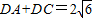 ,
,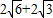 .
.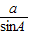 =
=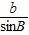 =
=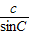 =2R;③如果圆为△ABC的内切圆,则根据面积公式S=
=2R;③如果圆为△ABC的内切圆,则根据面积公式S= •l•r(其中l表示三角形的周长).熟练掌握定理及公式是解本题的关键.
•l•r(其中l表示三角形的周长).熟练掌握定理及公式是解本题的关键. 

科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
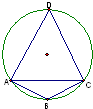 在半径为R的圆的内接四边形ABCD中,AB=
在半径为R的圆的内接四边形ABCD中,AB=| 3 |
| 3 |
| 1 |
| 4 |
| DA |
| DC |
查看答案和解析>>
科目:高中数学 来源:2010年江苏省盐城中学高考数学三模试卷(解析版) 题型:填空题
 .通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .
.通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .查看答案和解析>>
科目:高中数学 来源:2010年江苏省连云港市东海高级中学高考数学考前猜题试卷(4)(解析版) 题型:解答题
 .通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .
.通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com