
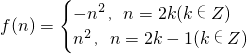 ,an=f(n)+f(n+1),则a1+a2+…+a100=________.
,an=f(n)+f(n+1),则a1+a2+…+a100=________. )×n+
)×n+ n2得S奇=(-3+1)×50-502=-350;
n2得S奇=(-3+1)×50-502=-350;

科目:高中数学 来源: 题型:
(08年聊城市四模文)(14分)已知函数![]() +
+![]() 数列{an}的首项为1,前n项和为Sn,且
数列{an}的首项为1,前n项和为Sn,且![]() ,在函数f(x)的图像上.
,在函数f(x)的图像上.
(1)证明:数列{an}是等差数列;
(2)若b=4,向量![]() 、
、![]() ,动点M满足
,动点M满足![]() ,点N是曲线
,点N是曲线![]() 上的动点,求|MN|的最小值.
上的动点,求|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源:2011年上海市虹口区高考数学一模试卷(文理合卷) (解析版) 题型:解答题
 ,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3.
,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3. ,设
,设 ,求g(n)的解析式及g(n)的最大值;
,求g(n)的解析式及g(n)的最大值;查看答案和解析>>
科目:高中数学 来源:2010年江苏省无锡市江阴市成化高级中学高考数学模拟试卷(18)(解析版) 题型:解答题
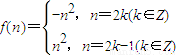 ,an=f(n)+f(n+1),则a1+a2+…+a100= .
,an=f(n)+f(n+1),则a1+a2+…+a100= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com