
【题目】设函数![]() ,
,![]() ,其中
,其中![]() 为实数.
为实数.
(1)若![]() 在
在![]() 上是单调减函数,且
上是单调减函数,且![]() 在
在![]() 上有最小值,求
上有最小值,求![]() 的取值范围;
的取值范围;
(2)若![]() 在
在![]() 上是单调增函数,试求
上是单调增函数,试求![]() 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
【答案】(1)![]()
(2)当![]() 或
或![]() 时,
时,![]() 的零点个数为1;当
的零点个数为1;当![]() 时,
时,![]() 的零点个数为2.
的零点个数为2.
【解析】
(1)∵![]() ,考虑到函数
,考虑到函数![]() 的定义域为
的定义域为![]() ,故
,故![]() ,进而解得
,进而解得
![]() ,即
,即![]() 在
在![]() 上是单调减函数. 同理,
上是单调减函数. 同理,![]() 在
在![]() 上是单调增函数.
上是单调增函数.
由于![]() 在
在![]() 是单调减函数,故
是单调减函数,故![]() ,从而
,从而![]() ,即
,即![]() .
.
令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
又![]() 在
在![]() 上有最小值,所以
上有最小值,所以![]() ,即
,即![]() ,
,
综上所述,![]() .
.
(2)当![]() 时,
时,![]() 必是单调增函数;当
必是单调增函数;当![]() 时,令
时,令![]() ,
,
解得![]() ,即
,即![]() ,
,
∵![]() 在
在![]() 上是单调函数,类似(1)有
上是单调函数,类似(1)有![]() ,即
,即![]() ,
,
综合上述两种情况,有![]() .
.
①当![]() 时,由
时,由![]() 以及
以及![]() ,得
,得![]() 存在唯一的零点;
存在唯一的零点;
②当![]() 时,由于
时,由于![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 上的图象不间断,∴
上的图象不间断,∴![]() 在
在![]() 是单调增函数,∴
是单调增函数,∴![]() 在
在![]() 上存在零点. 另外,当
上存在零点. 另外,当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上是单调增函数,
上是单调增函数,![]() 只有一个零点.
只有一个零点.
③当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() . ∴
. ∴![]() 是
是![]() 的最大值点,且最大值为
的最大值点,且最大值为![]() .
.
1)当![]() ,即
,即![]() 时,
时,![]() 有一个零点
有一个零点![]() .
.
2)当![]() ,即
,即![]() 时,
时,![]() 有两个零点. 实际上,对于
有两个零点. 实际上,对于![]() ,由于
,由于![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 上的图象不间断,∴
上的图象不间断,∴![]() 在
在![]() 上存在零点.
上存在零点.
另外,当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是单调增函数,∴
上是单调增函数,∴![]() 在
在![]() 上有一个零点.
上有一个零点.
下面需要考虑![]() 在
在![]() 上的情况,先证
上的情况,先证![]() ,
,
为此,我们要证明:当![]() 时,
时,![]() ,设
,设![]() ,则
,则![]() ,再设
,再设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是单调增函数,
上是单调增函数,
故当![]() 时,
时,![]() ,从而
,从而![]() 在
在![]() 上是单调增函数,进而当
上是单调增函数,进而当
![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,又
,又![]() ,且函数
,且函数![]()
在![]() 的图象不间断,∴
的图象不间断,∴![]() 在
在![]() 上存在零点.
上存在零点.
又当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 是单调减函数,所以,
是单调减函数,所以,![]() 在
在![]() 上只有一个零点.
上只有一个零点.
综上所述,当![]() 或
或![]() 时,
时,![]() 的零点个数为1;当
的零点个数为1;当![]() 时,
时,![]() 的零点个数为2.
的零点个数为2.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥AB,PA=1,PC=3,BC=2,sin∠PCA![]() ,E,F,G分别为线段的PC,PB,AB中点,且BE
,E,F,G分别为线段的PC,PB,AB中点,且BE![]() .
.
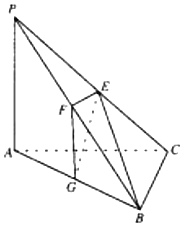
(1)求证:AB⊥BC;
(2)若M为线段BC上一点,求三棱锥M﹣EFG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块![]() 上划出一个三角形地块
上划出一个三角形地块![]() 种植草坪,两个三角形地块
种植草坪,两个三角形地块![]() 与
与![]() 种植花卉,一个三角形地块
种植花卉,一个三角形地块![]() 设计成水景喷泉,四周铺设小路供居民平时休闲散步,点
设计成水景喷泉,四周铺设小路供居民平时休闲散步,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,记
上,记![]() .
.
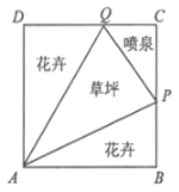
(1)当![]() 时,求花卉种植面积
时,求花卉种植面积![]() 关于
关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的最小值;
的最小值;
(2)考虑到小区道路的整体规划,要求![]() ,请探究
,请探究![]() 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题
①四面体![]() 中,
中,![]() ,
,![]() ,则
,则![]()
②已知双曲线![]() 的两条渐近线的夹角为
的两条渐近线的夹角为![]() ,则双曲线的离心率为2
,则双曲线的离心率为2
③若正数![]() 和
和![]() 满足
满足![]() ,则
,则![]()
④向量![]() ,若存在实数
,若存在实数![]() ,使得
,使得![]() ,则
,则![]()
其中真命题的序号是______(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是棱长为2的正方形,E为AD的中点,以CE为折痕把△DEC折起,使点D到达点P的位置,且点P的射影O落在线段AC上.
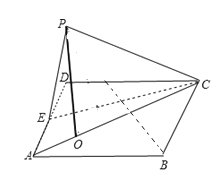
(1)求![]() ;
;
(2)求几何体P﹣ABCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数为![]() (α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ;
;
(1)写出曲线C的普通方程和直线l的参数方程;
(2)设点P(m,0),若直线l与曲线C相交于A,B两点,且|PA|![]() |PB|=1,求实数m的值.
|PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的![]() 名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取
名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取![]() 名学生的数学成绩(满分:
名学生的数学成绩(满分:![]() 分),并绘制成如图所示的茎叶图.将成绩低于
分),并绘制成如图所示的茎叶图.将成绩低于![]() 分的称为“不及格”,不低于
分的称为“不及格”,不低于![]() 分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
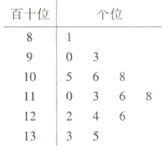
(1)估算此次联考该校高三学生的数学学科的平均成绩.
(2)估算此次联考该校高三学生数学成绩“不及格”和“优秀”的人数各是多少.
(3)在国家扶贫政策的倡导下,该地教育部门提出了教育扶贫活动,要求对此次数学成绩“不及格”的学生分两期进行学业辅导:一期由优秀学生进行一对一帮扶辅导,二期由老师进行集中辅导.根据实践总结,优秀学生进行一对一辅导的转化率为![]() ;老师集中辅导的转化率为
;老师集中辅导的转化率为![]() ,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
注:转化率![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com