
【题目】如图,在三棱锥P﹣ABC中,PA⊥AB,PA=1,PC=3,BC=2,sin∠PCA![]() ,E,F,G分别为线段的PC,PB,AB中点,且BE
,E,F,G分别为线段的PC,PB,AB中点,且BE![]() .
.
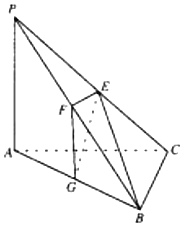
(1)求证:AB⊥BC;
(2)若M为线段BC上一点,求三棱锥M﹣EFG的体积.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证明PA⊥平面ABC,再证明BC⊥BP,即可得BC⊥平面PAB,即可得证;
(2)由BC∥平面EFG可得VM﹣EFG=VB﹣EFG=VE﹣BFG,证明EF⊥平面BFG后求出长度即可得解.
(1)证明:∵PA=1,PC=3,![]() ,∴PA⊥AC,
,∴PA⊥AC,
∵PA⊥AB,∴PA⊥平面ABC,
∴PA⊥BC,∵E为PC中点,且![]() ,∴BC⊥BP,∴BC⊥平面PAB,∴AB⊥BC;
,∴BC⊥BP,∴BC⊥平面PAB,∴AB⊥BC;
(2)∵E,F为中点,∴BC∥EF,且EF=1,由BC平面EFG,∴BC∥平面EFG,
∵M∈BC,∴VM﹣EFG=VB﹣EFG=VE﹣BFG,易知EF⊥平面BFG,FG∥PA,
![]() ,
, ![]() ,∴S△BFG
,∴S△BFG![]() ,
,
∴![]() .
.
∴三棱锥M﹣EFG的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数)。以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线
(t为参数)。以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,
,![]() 交于A,B两点,P点极坐标为
交于A,B两点,P点极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是线段EF上的动点
AC,P是线段EF上的动点
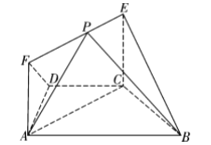
(1)求证:平面BCE⊥平面ACEF;
(2)求平面PAB与平面BCE所成锐二面角![]() 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市推行“共享汽车”服务,租用汽车按行驶里程加用车时间收费,标准是“1元/公里+0.2元/分钟”,刚在该市参加工作的小刘拟租用“共享汽车“上下班.单位同事老李告诉他:“上下班往返总路程虽然只有10公里,但偶尔上下班总共也需要用时大约1小时”,并将自己近50天往返开车的花费时间情况统计如下
时间(分钟) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
次数ξ | 8 | 18 | 14 | 8 | 2 |
将老李统计的各时间段频率视为相应概率,假定往返的路况不变,而且每次路上开车花费时间视为用车时间.
(1)试估计小刘每天平均支付的租车费用(每个时间段以中点时间计算);
(2)小刘认为只要上下班开车总用时不超过45分钟,租用“共享汽车”为他该日的“最优选择”,小刘拟租用该车上下班2天,设其中有ξ天为“最优选择”,求ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com