
【题目】设![]() 和
和![]() 是函数
是函数![]() 的两个极值点,其中
的两个极值点,其中![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 为自然对数的底数),求
为自然对数的底数),求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)先求![]() ,由已知条件得,方程
,由已知条件得,方程![]() =0有两个不等的正根
=0有两个不等的正根![]() ,则有
,则有![]() ,解得
,解得![]() ,结合韦达定理将
,结合韦达定理将![]() 变形为关于变量
变形为关于变量![]() 的函数表达式,
的函数表达式,![]() ,进而求值域得
,进而求值域得![]() 的取值范围;(2)将
的取值范围;(2)将![]() 变形为
变形为![]() ,为了减少参数,将
,为了减少参数,将![]() 代入得,
代入得,![]()
![]() ,为了便于求值域,利用
,为了便于求值域,利用![]() ,继续变形为
,继续变形为![]()
![]() ,设
,设![]() ,通过还原,将
,通过还原,将![]() 表示为变量
表示为变量![]() 的函数,进而求值域即可.
的函数,进而求值域即可.
(1)函数f(x)的定义域为(0,+∞),f′(x)![]() ,
,
依题意,方程x2﹣(m+2)x+1=0有两个不等的正根a、b(其中a<b),
故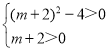 ,∴m>0,
,∴m>0,
又a+b=m+2,ab=1,
∴f(a)+f(b)=lnab![]() (m+2)(a+b)
(m+2)(a+b)
![]() (m+2)(a+b)
(m+2)(a+b)![]() ,
,
∵m>0,∴![]() (m+2)2﹣1<﹣3,
(m+2)2﹣1<﹣3,
故f(a)+f(b)的取值范围是(﹣∞,﹣3);
(2)当m![]() 2时,(m+2)2≥e
2时,(m+2)2≥e![]() 2,
2,
设t![]() (t>1),则(m+2)2=(a+b)2
(t>1),则(m+2)2=(a+b)2![]() t
t![]() e
e![]() 2,
2,
∴t![]() e
e![]() (t﹣e)(1
(t﹣e)(1![]() )≥0,∴t≥e,
)≥0,∴t≥e,
∴f(b)﹣f(a)=ln![]() (b2﹣a2)﹣(m+2)(b﹣a)
(b2﹣a2)﹣(m+2)(b﹣a)
=ln![]() (b2﹣a2)﹣(b+a)(b﹣a)=ln
(b2﹣a2)﹣(b+a)(b﹣a)=ln![]() (b2﹣a2)
(b2﹣a2)
=ln![]() (
(![]() )=ln
)=ln![]() (
(![]() )=lnt
)=lnt![]() (t
(t![]() ),
),
构造函数g(t)=lnt![]() (t
(t![]() ),其中t≥e,
),其中t≥e,
由g′(t)![]() (1
(1![]() )
)![]() 0
0
∴g(t)在[e,+∞)上单调递减,g(t)≤g(e)=1![]() ,
,
故f(b)﹣f(a)的最大值为1![]() .
.


科目:高中数学 来源: 题型:
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是中国成立70周年,也是全面建成小康社会的关键之年.为了迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手答题得分情况,则下列说法正确的是( )
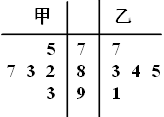
A.甲组选手得分的平均数小于乙组选手的平均数B.甲组选手得分的中位数大于乙组选手的中位数
C.甲组选手得分的中位数等于乙组选手的中位数D.甲组选手得分的方差大于乙组选手的的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资![]() 、
、![]() 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,![]() 产品的利润
产品的利润![]() 与投资量x成正比例,其关系如图1,
与投资量x成正比例,其关系如图1,![]() 产品的利润
产品的利润![]() 与投资量x的算术平方根成正比例,其关系如图2;(利润与投资量单位:万元)
与投资量x的算术平方根成正比例,其关系如图2;(利润与投资量单位:万元)
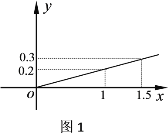
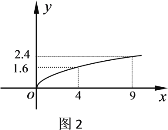
(1)分别将![]() 、
、![]() 两产品的利润表示为投资量的函数关系式;
两产品的利润表示为投资量的函数关系式;
(2)该公司已有20万元资金,并全部投入![]() 、
、![]() 两种产品中,问:怎样分配这20万元投资,才能使公司获得最大利润?其最大利润为多少万元?
两种产品中,问:怎样分配这20万元投资,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥AB,PA=1,PC=3,BC=2,sin∠PCA![]() ,E,F,G分别为线段的PC,PB,AB中点,且BE
,E,F,G分别为线段的PC,PB,AB中点,且BE![]() .
.
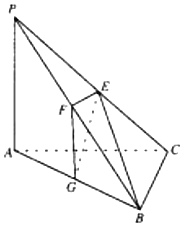
(1)求证:AB⊥BC;
(2)若M为线段BC上一点,求三棱锥M﹣EFG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块![]() 上划出一个三角形地块
上划出一个三角形地块![]() 种植草坪,两个三角形地块
种植草坪,两个三角形地块![]() 与
与![]() 种植花卉,一个三角形地块
种植花卉,一个三角形地块![]() 设计成水景喷泉,四周铺设小路供居民平时休闲散步,点
设计成水景喷泉,四周铺设小路供居民平时休闲散步,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,记
上,记![]() .
.
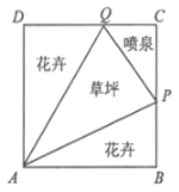
(1)当![]() 时,求花卉种植面积
时,求花卉种植面积![]() 关于
关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的最小值;
的最小值;
(2)考虑到小区道路的整体规划,要求![]() ,请探究
,请探究![]() 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com