Question

【题目】设分别是椭圆的左、右焦点．

(1)若是该椭圆上的一个动点，求的最大值和最小值；

(2)设过定点的直线与椭圆交于不同的两点，且为锐角(其中为坐标原点)，求直线的斜率的取值范围．

Answer 1

【答案】（1） ；（2）.

【解析】

(1)设出点P的坐标，向量坐标化得到的表达式，进而得到最值；（2）为锐角即，设出点AB的坐标，向量坐标化得到点积的表达式为：x1x2＋y1y2,联立直线和椭圆方程，由韦达定理得到结果.

(1)由已知得，F1(－，0)，F2(，0)，设点P(x，y)，

则＋y2＝1，且－2≤x≤2．

所以·＝(－－x，－y)·(－x，－y)＝x2－3＋y2＝x2－3＋1－＝x2－2，

当x＝0，即P(0，±1)时，(·)min＝－2；

当x＝±2，即P(±2，0)时，(·)max＝1．

(2)由题意可知，过点M(0，2)的直线l的斜率存在．

设l的方程为y＝kx＋2，

由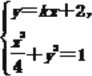消去y，化简整理得

(1＋4k2)x2＋16kx＋12＝0，Δ＝(16k)2－48(1＋4k2)＞0，解得k2>．

设A(x1，y1)，B(x2，y2)，则x1＋x2＝－，x1x2＝，

又∠AOB为锐角，所以·＞0，即x1x2＋y1y2＞0，

有x1x2＋(kx1＋2)(kx2＋2)＝(1＋k2)x1x2＋2k(x1＋x2)＋4

＝(1＋k2)·＋2k·＋4＞0，解得k2＜4，

所以＜k2＜4，即k∈．